Summary of elementary tactics

In the previous lecture, we considered some elementary tactics, with no or only very little automatisation. Here is a reminder:

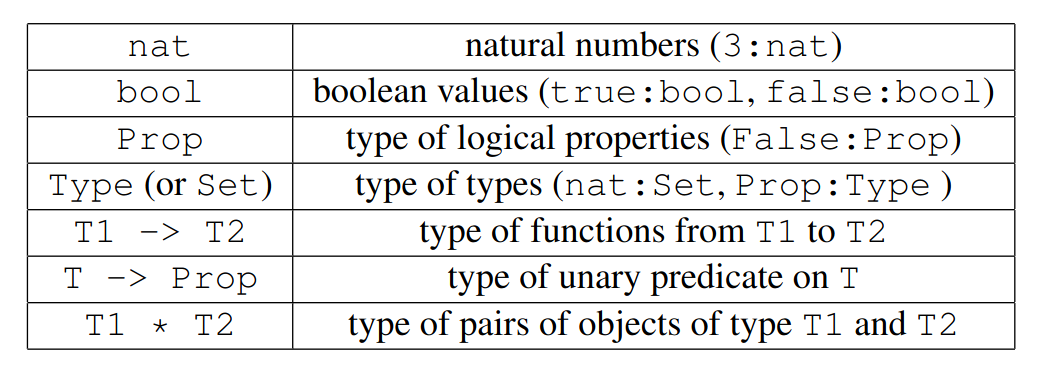
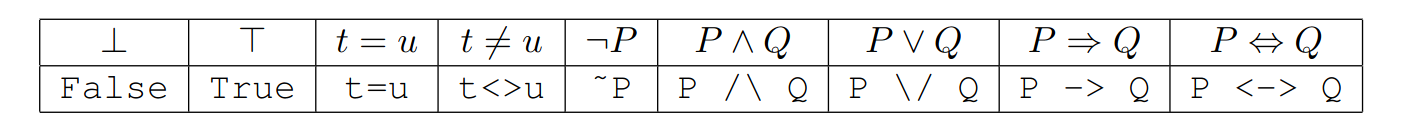
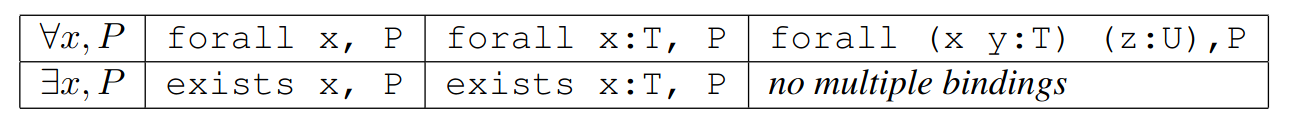
• assumption if the current goal is exactly one of the hypothesis (cf. the axiom rule in logic).
• For all primitive connectors (quantification ∀, implication →):
  • introduction via intro (or one of its variants intros,
  intro x, intros x y ...)
  • elimination via apply H (where H is the name of
  the hypothesis to eliminate).
• The other connectors (which are actually inductive definitions) may ideally be introduced by constructor and eliminated by destruct H. But the introduction frequently requires more ad-hoc tactics:
  • split for a conjunction ∧ (written /\)
  • left and right for a disjunction ∨ (written \/)
  • ∃ ... (written exists) for a quantification ∃
  (where ... is the place where the existential witness is given)
  • No introduction tactic for False !
  • For True (seldom used in Coq), the introduction can
  be done via constructor, but nothing to eliminate.
• The simpl tactic performs a conversion on the goal.
• In Coq, a definition d could be replaced by its body thanks to the tactic unfold d.
• Some abbreviations:
  • A negation ¬A (written ~A) is just a shortcut for A→False.
  Hence introduction via intro (or intros a, giving a name forces the introduction) and elimination via apply H or destruct H (whether one wants to focus on the underlying → or False).
  • An equivalence A↔B (written A<->B) is just a shortcut for (A→B)/\(B→A),
  hence is manipulated as a conjunction of implications.
• Some automatic tactics : trivial, easy, auto, eauto, intuition, firstorder. See the Coq documentation for more details.

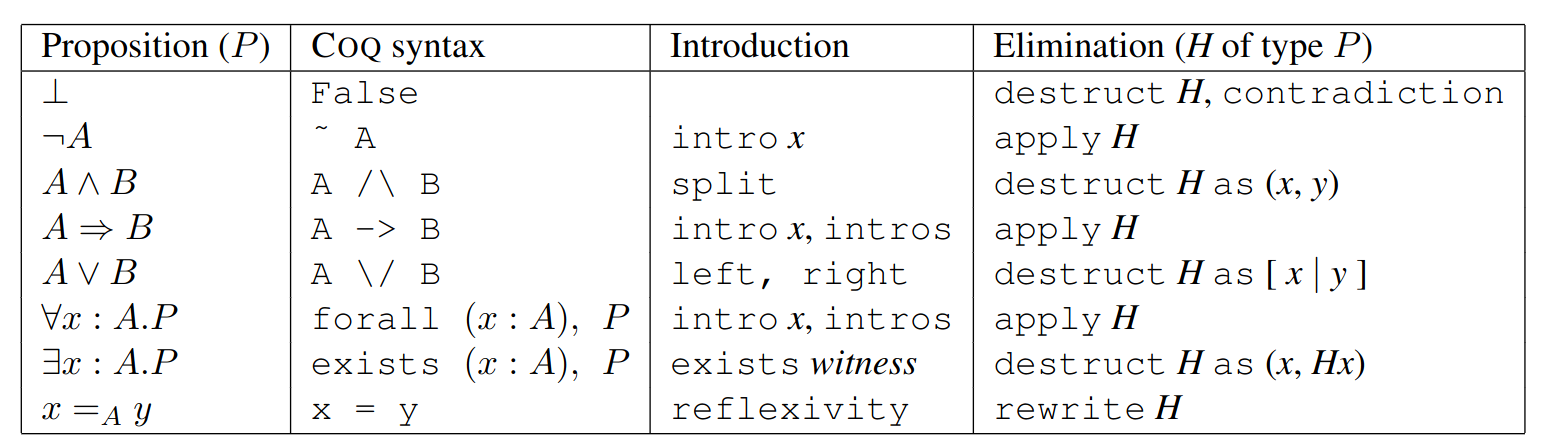
Today's program

Today, we will mostly focus in equality and induction plus some additional useful features. Here is a little warm-up betfore we enter the details: The equality is handled by tactics:

• reflexivity
• symmetry
• transitivity ... (where you need to give the intermediate

term) and

• rewrite ... (give the equality name or lemma to use as a

rewrite rule) or

• rewrite <- ... (right-to-left rewriting)

Inductive reasoning will be studied at length in coming lectures. Just to state it immediately:

• induction ... (to do inductive reasoning, to be investigated in the next lectures).

Managing the interactive proof progresses

• Undo: goes back one tactic
• Restart: restart the proof from the original goal
• Abort: Aborts the current proof.
• Admitted: gives up the current proof and declares the initial goal as an axiom.
• Focusing using bullets or i: { tac }
• Applying a tactic to the i-th goal: i:tac, ...
• Modifying the goal list: all: swap i j
• Getting information:
  • Show display the current goals;
  • Show Proof displays the current proof term (with holes for open goals).

Composing tactics

Some more:

• tac ;[tac1 |. . .|tacn]: applies tac to the goal which generates n subgoals and taci is applied to the i-th subgoal.
• idtac: always succeed, leaving the goal unchanged.
• fail: always fail (useful to implement a tactic saying: "I solve the goal immediatly or I fail" with tac; fail. Indeed, if tac fails, it fails, if tac succeeds producing at least one subgoal, it fails and if tac suceeds producing no subgoal, it succeeds.
• try: it behaves like tac || idtac. It is often useful to do tac ; try tac'. Another example is tac; try (tac'; fail). this tries applying tac' to the subgoals generated by tac but only to those which are completely solved by tac', leaving the other ones unchanged.

A tiny bit of automation: auto and trivial

auto recursively composes intros, apply and assumptions until a given depth (by default, it is 5). Either it completely solves the goal, or it leaves the goal unchanged. trivial is less powerfull that auto but it emphasizes that concluding is easier.

Searching for Lemmas

It is possibl to search by describing a pattern of what you are looking for:

also non linear patterns:

Searching only for equalities:

Equality: eq

Syntactic equality : only x is equal to x

Inductive eq (A : Type) (x : A) : A -> Prop :=  eq_refl : eq A x x.

constructor is the reflexivity rule. tactic "reflexivity"

The Leibniz principle, or the rewrite principle :

eq_ind
     : forall (A : Type) (x : A) (P : A -> Prop),
       P x -> forall y : A, x = y -> P y

match on a equality is a form of rewrite the rewrite tactic proceed by a match on the equality

rewriting equalities

If H : a = b is in the context, then rewrite H rewrites occurrences of a into b On the other hand, rewrite <- H rewrite bs into as.

It is possible to rewrite in an hypothesis with rewrite H in H'.

The pattern tactic:

When there are multiple occurrences of a terme and one wants to rewrite just one, the pattern tactic comes in handy: pattern t at i j k.

Conditional rewrites

When using a rewrite on a conditional goal, that may generate subgoals.

nat and induction

2+2 = Nat.add (S (S 0)) 2.
    = match S (S 0) with
      | 0 => m
      | S p => S (add p 2)
     (* unfold rule for fixpoint : a fixpoint applied to a constructor can
        unfold once *)
    = S (add (S 0) 2)
    = ...
    = 4