Course5 : Proofs as Programs, Types as Propositions (+ Some complements on dependent types in Coq)

Preliminaries

The Coq file supporting today's course is available at https://gitlab.math.univ-paris-diderot.fr/saurin/pf2-lmfi-2024/-/blob/main/Lecture/Course5.v. And the standalone exercise sheet is available at: https://gitlab.math.univ-paris-diderot.fr/saurin/pf2-lmfi-2024/-/blob/main/TP/TP5.v. Today, we shall first pursue the study of dependent types and vectors in particular. Then, we will put in practice the concepts introduced so far in order to set up the proof framework of Coq by doing putting in practice the Curry-Howard correspondence.

Inductive dependent types

Vectors

Let us sum up what we studied last week on vectors using an inductive type definition to define a dependent type, that is an inductive dependent type:

Note that the n argument of Vcons is still there internally and can be printed by requiring to print all information (in CoqIDE, this is managed in the "View" panel):

Conversion bewteen vectors and regular lists.

Naive length function:

We could more simply define it as:

Head and tails in vectors

With such vectors, we avoid the usual issues encountered when defining head and cons on lists, requiring to use a default value or an option type. Indeed, we can specify that we want to operate only on non-empty vectors, since they have a Vect A (S n) type for some n. On lists we can define the head function using a default value:

Or returning in the option A type:

On vectors, we can more simply restict the domain of the function Vhead:

Notice that the match branch for Vnil just vanished, and Coq did not complained about a missing case ! Actually, there does exist such a case internally, filled by Coq with a somewhat arbitrary code, that will never be accessed during computations.

Some check to see what is going on with the missing branch:

The error message is: The term "Vnil" has type "vect ?A 0" while it is expected to have type "vect ?A (S ?n)". That is, there is a type mismatch.

Concatenating vectors

Everything goes smoothly here, since this function mimics the equations of the addition on nat.

0 + m = m S p + m = S (p+m)

of type vect A m = vect A (0+m) = vect A (n+m) here

of type vect A (S (p+m)) = vect A ((S p)+m) = vect A (n+m) here

Alas, the situation is not always so smooth. Let us first consider the following two possible definitions for concatenating three vectors:

What can we say about their types ? for other algorithms, we are not so lucky. For instance, consider the (naive) definition of the reverse of a vector. A direct attempt is rejected as badly-typed:

Which returns the following error message: The term "Vapp (Vrev A n0 v0) (Vcons x Vnil)" has type "vect A (n0 + 1)" while it is expected to have type "vect A (S n0)". In order to accept such a definition, Coq would need to know that vect A (n+1) is equal to vect A (1+n). This is provably true, but not computationally true (a.k.a "convertible" in the Coq jargon) since n is not instantiated in a concrete natural number. More precisely, we cannot have n+1 = 1+n by just the above (Peano) equations as they require n to start with a constructor to reduce in the left-hand side, this will be handeled later by using a proof by induction. We shall come back to vectors later, when we have seen enough about proofs in Coq to be able handle this issue in detail. Let us review quickly a potential solution, just to convince you that there are workarounds.

But for defining our Vrev, we need a proof of n+1=1+n.

That is a lemma called Nat.add_1_r, exactly what we need: remember indeed that 1 + n reduces to S n

This definition is not yet a satisfactory solution, and we will improve it when we have more tools and concepts at hands. As a temporary conclusion on vectors:

• programming with dependent type may help a lot by ruling out some impossible cases and producing functions with rich types describing precisely the current situation.
• but it is not always convenient to proceed in this style, and may be stuck in defining even some programs as simple as reversing a vectore with this Vrev.
• programming with dependent types requires proving as we program.

Some more details about dependent types

Perfect binary trees, this time via inductive types.

Just as vectors can be compared to lists, we add an extra argument in nat to obtain perfect binary trees, here encoding the depth of the tree.

Again, arguments of constructors may be treated implicitly:

Dependent pairs (aka. dependent sums).

We have seen that the arrow type A→B has a dependent counterpart, the product ∀ x:A, B x (also called Π-type). Similarly, the pair type A×B, has a dependent version which is called sigT (for Σ-type), with a notation {x:A & B x}.

Inductive sigT (A : Type) (P : A → Type) : Type := existT : ∀ x : A, P x → {x : A & P x}. which is the inductive type, with syntax { ... & ... }

and its constructor

Just as the conclusion of a product may have a type B x which depends on the value x of the input, here the right component of this pair {x:A & B x} will have a type B x which depends on the value x present on the left of this pair. As the name existT of the constructor may suggests, this type can also be seen as an existential type : "there exists an x in A such that the right component is in B x". Example : a type of all perfect binary trees on a domain A, regardless of theirs depth

Alternative definition without the notation:

We can exhibit an inhabitant of this sum type, that is the pair of an m: nat and an inhabitant of fultree A m.

the _ is here the "predicate" B, that Coq can infer here as being fulltree nat. Actually, Coq could even guess here the second argument (1), by typing the last one (obtaining fulltree A 1 here).

To manipulate dependent sums, we have some predefined projections:

of type : (fun n : nat => fulltree nat n) (projT1 some_fulltree) which is convertible to : fulltree nat 1

See TD : we could redo the start of TD4, this time ensuring *by typing* that all the trees we manipulate are perfect :

For instance :

We will see later a few other existential types :

• the type of existential statements ∃ x:A, B x where A and B are in universe Prop.
• the "mixed" existential type {x:A | B x} (with underlying type name sig), where B is a logical statement in Prop, but A is in Type (we call A an "informative" or "relevant" type).

Fin: finite sets

Another famous dependent type : type Fin n, encoding a canonical finite set with exactly n elements. Or said otherwise, the type of all numbers strictly less than n. So this type is also called the "bounded integers".

As usual, let us get rid of some "boring" arguments

Nobody can be in type Fin 0, since all constructors of Fin have final types of the form Fin (S ...). Then Fin 1 is a type with just one element

Then Fin 2 is a type with two elements, but no more

If we convert inhabitants of Fin n back to nat by forgetting all the inner implicit arguments, then we indeed get all nat numbers strictly less than n.

Note : another approach for defining such "bounded" integers is to use an existential type to restrict nat.

• Pros : easy projection to nat, no need for a reconstruction like fin2nat above.
• Cons : This implies to work with logical predicate < (in Prop, not the boolean comparison <? we have been using up to now) and requires to build arithmetical proofs. This is hence less suitable for the Vnth function below (no nice inductive structure).

Application: Vnth

The type Fin of "bounded" integers provides a neat way to specify and implement a safe access to the n-th element of a vector (type vect), recall: Inductive vect' (A:Type) : nat → Type := | Vnil : vect' A 0 | Vcons n : A → vect' A n → vect' A (S n). Arguments Vnil {A}. Arguments Vcons {A} {n}. For a vector v in type vect A n, we can access any position p as long as p is in Fin n (hence garanteed to represent a number strictly less than n.

Notice that this type of programming is still relatively new in Coq, and still very fragile. For instance, in the previous example, one may be tempted to move the recursive call Vnth inside the final match v, and hence write: | Succ p => fun v => match v with Vcons _ v => Vnth p v end But this is rejected by Coq for the moment. Similarly, no way (yet ?) to move out the two fun v ⇒ and factorize them in one fun v ⇒ outside of match p. Example of use: with a vector of size 3, one may access to elements at position 0, 1, 2 but not 3.

Using Coq as a proof assistant.

At last, we shall start using Coq as a proof assistant. But before really doing so, we shall see that in fact, we already have all we need to do this with what you learnt from the start of the semester! The present section shall thus be seen as a pedagogical introduction to modelling from scratch proofs as Coq programs, that is really putting Curry-Howard correspondence at work, before really considering how this is actually done in Coq. In order to prevent mixing Coq actual features with our own development, I use french terms in this introductory part, which will also be an occasion for practicing french for some of you! To start with, we set implicit arguments to lighten notations and we define Formulas as an alias for Set. (this will be updated later!)

In the following, we shall introduce some types and type constructions in Formula as well as some Coq terms which shall model inference rules on them. We shall follow the outline:

• true
• false
• implication
• negation
• conjunction
• disjunction
• excluded-middle
• quantifiers
• equality
• first proofs

Let us consider the following inductive types:

Constant True

with its single constructor (introduction rule):

VRAIintro : VRAI VRAI has essentially one proof (inhabitant): its single constructor.

Constant False

with no constructor (no introduction rule) and a generic destructor, eliminating to any formula:

Having no constructor, FAUX has no introduction rule.

Notice the odd shape of this pattern-matching with no clause for matching... but indeed FAUX has no constructor!

FAUXelim : ∀ A : Formula, FAUX → A FAUXelim corresponds to the elimination of the absurd, also known as ex falso sequitur quodlibet.

Implication

with its constructor / introduction rule (if from assuming A, I can deduce B, then I can deduce A => B), and its destructor / elimination rule (Modus Ponens):

IMPintro : ∀ A B : Formula, (A → B) → IMP A B

IMPelim : ∀ A B : Formula, IMP A B → A → B Notice that an alternative, would have been to define IMP simply as an alias for → :

We will come back to this later today.

Negation :

with its introduction rule and its elimination rule (from not A and A, deduce false):

NEGintro : ∀ A : Formula, (A → FAUX) → NEG A

NEGelim : ∀ A : Formula, NEG A → A → FAUX Negation could also be considered as a defined connective:

Conjunction

with its constructor (introduction rule) and its two destructors (elimination rules) :

ETintro : ∀ A B : Formula, A → B → ET A B

ETelim2 : ∀ A B : Formula, ET A B → B

Equivalence

Now that we have disjunction, equivalence can be obtained as a defined connective:

Disjunction

with its two constructors (introduction rule) and its elimination rule:

OUintro1 : ∀ A B : Formula, A → OU A B

OUelim : ∀ A B C : Formula, OU A B → (A → C) → (B → C) → C

Shall a proof of a disjunction only be obtained from a proof of the left disjunct or from the right disjunct? Is there no third option? The excluded-middle is a third option, if you want to accept it. But there is no computational counter-poart to it: one shall add it as an axiom, that is as an additional constant we declare. Do you remember how to do it?

Excluded middle :

What is this term PeirceLaw ??

Quantifiers:

We now introduce formula constructions and deduction schemas for quantifiers. Both for the universal and existential quantifier, we provide two versions of the quantifiers:

• an arithmetical quantification and
• a general quantification over any type in Set.

Forall qantifier

PTNintro : ∀ B : nat → Formula, (∀ x : nat, B x) → POURTOUTN B

POURTOUTNelim : ∀ B : nat → Formula, POURTOUTN B → ∀ t : nat, B t

Exists quantifier

IENintro : ∀ (B : nat → Formula) (x : nat), B x → ILEXISTEN B Be careful in reading this type!! Let us add some parentheses: IENintro : ∀ (B : nat → Formula) (x : nat), (B x → ILEXISTEN B)

ILEXISTENelim : ∀ (B : nat → Formula) (C : Formula), ILEXISTEN B → (∀ x : nat, B x → C) → C Again, it is useful to add some parentheses to parse the above type correctly: ILEXISTENelim : ∀ (B : nat → Formula) (C : Formula), ILEXISTEN B → (∀ x : nat, (B x → C)) → C

Equality

The only introduction rule for equality is the reflexivity of equality. Using equality amounts to substituting equals by equals and this is dealt with through dependent pattern-matching.

EQNintro : ∀ x : nat, EQN x x

EQNelim : ∀ (A : nat → Set) (m n : nat), EQN m n → A m → A n

One can state and prove the first properties about equality :

One can state and prove the first properties about equality even over other individual sorts:

Even and Odd numbers

We shall end this introduction with some more complex statements and proof, involving inductive reasoning. Let us first define two predicates over nat modelling that an natural number is even (resp. odd):

It is natural to be willing to prove that any natural is even or odd. Let us do it !

EvenOrOdd : (∀N) (fun n : nat ⇒ Even n ∨ Odd n)

SKIP THIS!!

Commutativity of addition.

AddComm : (∀N) (fun m : nat ⇒ (∀N) (fun n : nat ⇒ m + n == n + m))

Encounter with the third kind: Prop

Since the start of the semester, we worked with a first universe hierarchy (Type(i), i in |N) (and Set is Type(0).

Alias for the first level Type(0)

The various levels of the hierarchy are used to "type types":

Set is Type(0)

Here, Type is Type(1)

Here, Type is Type(1)

Here, Type → Type : Type should be read Type(i) → Type(j) : Type(max(i,j)+1 Since Type(i) : Type(i+1) and Type(j) : Type(j+1)

Another universe : Prop The universe of logical statement and proofs

is the canonical proof of True, hence I : True

Back to the type hierarchy

                Type(...)
                   |
                 Type(3)
                   |
                 Type(2)
                   |
                 Type(1)
               /         \
             /            \
           /               \
Set=Type(0)                Prop
 /   |     \               |   \
nat bool bool->nat       True  False
 |   |       \             |
 O   true    \             I     -  (no closed proof of False)
      (fun (x:nat) => 1)           

An upward link between T and S represents the fact that one can derive T : S in Coq type system. In Coq, the arrow type A→B is actually not a primitive construction, it is a particular case of a product ∀x:A,B (Coq syntax ∀ x:A, B). When variable x does not occur in B (non-dependent product), we write A→B. For a first example of dependent product, see the definition of identity below. Roughly, the typing rule for a product looks like :

• If Γ ⊢ A:Type and Γ+x:A ⊢ B:Type then Γ ⊢ (∀ x:A,B) : Type

In reality, one must take care of the indices of the Type universes : the rightmost index is the max of the other two indices:

• If Γ ⊢ A: Type(i) and Γ+x:A ⊢ B:Type(j) then Γ ⊢ (∀ x:A,B) : Type(max(i,j))

Or, written as an inference rule:

Γ ⊢ A:Type(i)         Γ+x:A ⊢ B:Type(j)
________________________________________(Prod-Type)
  Γ ⊢ (forall x:A,B) : Type(max(i,j))

Prop has some specificities that we shall investigate below in more details.

Terminology about Set vs Prop

• In Set:
  • A specification is any type S of the sort Set
  • A program is any term t the type of which is a specification.
• In Prop:
  • A proposition or statement is any type P of the sort Prop
  • A proof is any term t the type of which is a proposition.

To sum up: A program is an inhabitant of a specification while a proof is an inhabitant of a proposition.

Rules for forming dependent product in the Calculus

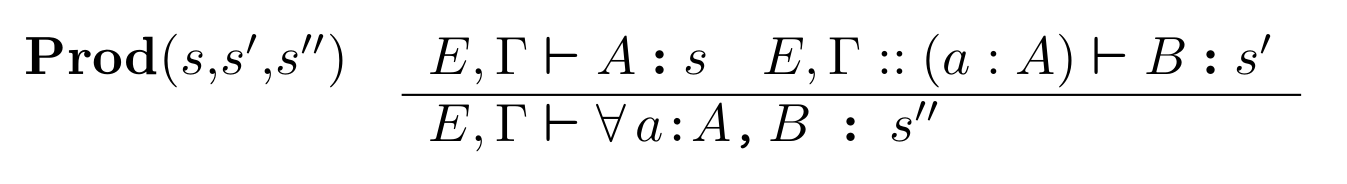
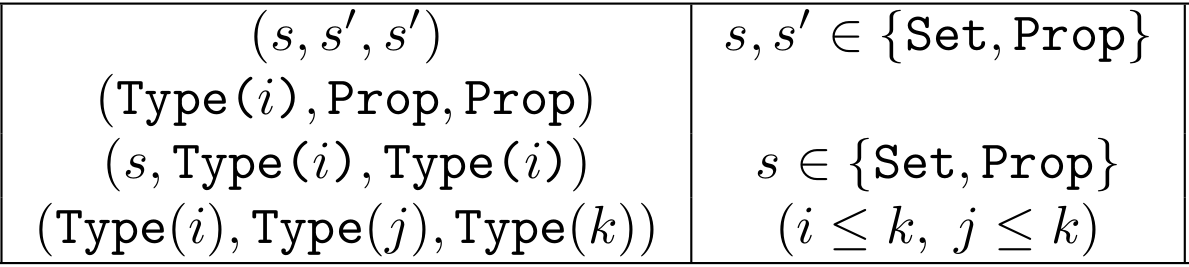
of Constructions: The above lines respectively correspond to:

• simple types
• impredicativity of Prop
• dependency
• higher-order

Stating theorems and proving them using Coq

Entering the proof mode

The user indicates she wants to start a proof with a command such as : Lemma and_commut : ∀ A B : Prop, A ∧ B ↔ B ∧ A. This command gives a name (here and_commut) to the lemma, this will allow later to refer to this lemma later. Instead of Lemma, one can use similar keywords such as Theorem or Proposition or Fact: they are all equivalent form the point of view of Coq and are used to help the human reader to follow a formal proof development, as in common mathematical texts. After that, the command Proof. is to be used to mark the actual beginning of the proof itself (actually not mandatory but strongly recommanded).

Subgoals and tactics

When a proof is started, the proof mode of Coq will display in the higher right part one or several subgoals that are to be proved separately, one by one. These subgoals are essentially sequents of the natural deduction logic, written vertically : the (named) hypothesis comes first on top and the conclusion is below the bar. In the upper part one can also find the variable declarations. The proof is to be done by tactics, that are orders given by the user to progress in the proof of the current goal, by transforming this goal in various ways. Tactics have lowercase names. For instance, the intro tactic performed on a goal of the form A → B will introduce an hypothesis H : A in the context, and replace the conclusion by B. Each inference rule of the natural deduction logic will correspond to one tactic (or more), but some tactics allow to perform more advanced proof steps, for instance solving linear inequalities in the Presburger arithmetic (tactic lia). Each tactic may generate several subgoals (corresponding to premises of the underlying logical rule), or on the contrary it may completely solve the current goal and hence remove it. The proof is finished when all subgoals are proved. In this case, the command Qed is to be used (from Quod erat demonstrandum) to conclude the proof and leave the proof mode. Here comes a possible complete proof for the previous statement:

When tactics are separated by dots, Coq will execute them steps-by-steps. One can also use semi-colon ; to chain tactics : the second tactic is applied to all subgoals resulting from the first tactic on the current goal, and so forth. For instance, split;assumption applies assumption on the two subgoals created by split. Before a tactic, one may optionally write a bullet, i.e. one of the character - or + or ×. These bullets help organizing the proof in a hierarchical way, with delimitation of each sub-part (enforced by Coq). Such a proof script is to be saved in a file with a .v extension, as done in the previous lectures for instance myproofs.v. Then it can be compiled via the unix command coqc myproofs.v. If the content of this file is correct, then a binary file myproofs.vo is produced, allowing later a fast reload of our proofs (via the Require Import command).

A detailed study of Coq's built-in logical propositions.

We shall now redo what we did in the first part of this lecture, but using Coq natively defined types. You should experience some déjà vu but there will be some difference (mainly for implication and quantification).

Just about the same as this: Definition my_first_proof_bis : True := I. Operators, for building more advanced statements

->, implication

or step by step : intro : the tactic of introduction of -> :

  A |- B
-----------(->intro)
 |- A-> B 

to inspect the proof term being built

the axiom rule of natural deduction

forall, the dependent version of the ->

Same introduction tactic : intro.

forall and its non-dependent version -> are the only primitive operators. To introduce them, one has the following introduction tactics: intro / intros / intros ... It is possible to name the hypothesis or quantified variables, otherwise, Coq name them automatically: it can be convenient but may result in less maintainable formal proofs. On the other hand, in order to used an implicative of universally quantified statement, one uses their elimination: apply H.

assumption. apply a.

By default, apply work on the goal to be prove, it is backward-chaining, proving from the conclusion to the hypothesis. But one can also specify that apply should be used on an hypothesis, reasoning in forward-chaining mode, from the hypotheses to the conclusion:

assumption. apply a.

Other operators

True

False

no closed construction

elimination of a False hypothesis

Compare with the predifined :

negation is a shortcut for ...->False

Lemma attempt : ~True. Proof. unfold "~" in *. intro.

/\, conjunction

• introduction is done via the split tactic
• elimination via destruct ...

or destruct H as [HA HB].

Check and_ind. Available bullets for structuring a proof script : - + ×

\/, disjunction

• introduction is done via the left and right tactics
• elimination via destruct ...

or destruct H as [HA | HB].

<-> equivalence

A<->B is just a shortcut for (A->B)/\(B->A)

exists : introduction via : exists ... elimination via : destruct ...

Summary of elementary tactics

• assumption if the current goal is exactly one of the hypothesis (cf. the axiom rule in logic).
• For all primitive connectors (quantification ∀, implication →):
  • introduction via intro (or one of its variants
  intros, intro x, intros x y ...)
  • elimination via apply H (where H is the name of
  the hypothesis to eliminate).
• The other connectors (which are actually inductive definitions) may ideally be introduced by constructor and eliminated by destruct H. But the introduction frequently requires more ad-hoc tactics:
  • split for a conjunction ∧ (written /\)
  • left and right for a disjunction ∨ (written \/)
  • ∃ ... (written exists) for a quantification
  ∃ (where ... is the place where the existential witness is given)
  • No introduction tactic for False !
  • For True (seldom used in Coq), the introduction can
  be done via constructor, but nothing to eliminate.
• Some abbreviations:
  • A negation ¬A (written ~A) is just a shortcut
  for A→False. Hence introduction via intro (or intros a, giving a name forces the introduction) and elimination via apply H or destruct H (whether one wants to focus on the underlying → or False).
  • An equivalence A↔B (written A<->B) is just a
  shortcut for (A→B)/\(B→A), hence is manipulated as a conjunction of implications.
• Some automatic tactics : trivial, easy, auto, eauto, intuition, firstorder. See the Coq documentation for more details.

In today practical session, you will first try to prove the statements with no or little automatisation, and then experiment with these tactics in a second time. Indeed, it can be helpful later to know how to proceed steps-by-steps, since real-life proofs are seldom doable by just automatic tactics.

Some more tactics

In Coq, a definition d could be replaced by its body thanks to the tactic unfold d. The equality is handled by tactics:

• reflexivity
• symmetry
• transitivity ... (where you need to give the intermediate term) and
• rewrite ... (give the equality name or lemma to use as a rewrite rule) or
• rewrite <- ... (right-to-left rewriting)

Inductive reasoning will be studied at length in coming lectures. Just to state it immediately:

• induction ... (to do inductive reasoning, to be investigated in the next lectures).