Les arbres rouges et noirs sont une variante des arbres binaires de recherche. Leur intérêt principal est qu'ils sont relativement équilibrés. On considère ici des arbres binaires de recherche où les valeurs sont portées par les nœuds internes. Les feuilles ne sont pas prises en compte dans la hauteur de l'arbre.
Un arbre rouge et noir est un arbre binaire de recherche ou chaque nœud est de couleur rouge ou noire de telle sorte que
La première condition est simplement technique et sans grande importance. La seconde condition stipule que les nœuds rouges ne sont pas trop nombreux. La dernière condition est une condition d'équilibre. Elle signifie que s'il on oublie les nœuds rouges d'un arbre on obtient un arbre binaire parfaitement équilibré.
Dans un arbre rouge et noir, on peut toujours supposer que la racine est noire. Si elle est rouge, on change sa couleur en noire et toutes les propriétés restent vérifiées.
Un arbre binaire complet de hauteur h possède au plus 1 + 2 + … + 2h = 2h+1-1 nœuds internes. Autrement dit, un arbre ayant n nœuds internes est de hauteur au moins égale à ln(n+1)-1. La hauteur minimale d'un arbre à n nœuds internes est atteinte lorsque l'arbre est parfaitement équilibré et que feuilles sont toutes sur un ou deux niveaux.
ln(n+1)-1 ≤ h.
Les arbres rouges et noirs sont relativement bien équilibrés. La hauteur d'un arbre rouge et noir est de l'ordre de grandeur de ln(n) où n est le nombre d'éléments dans l'arbre. En effet, la hauteur h un arbre rouge et noir ayant n éléments vérifie l'inégalité
h ≤ 2ln(n+1).
Pour un arbre rouge et noir, on appelle hauteur noire le nombre k de nœuds internes noirs le long d'une branche de la racine à une feuille. On montre par récurrence sur cette hauteur noire, qu'un arbre de hauteur noire égale à k possède au moins 2k-1 nœuds internes. Si cette hauteur noire vaut 0, l'arbre est réduit à une seule feuille et il ne possède aucun nœud interne. Si un arbre est de hauteur noire égale à k > 0, alors ses sous-arbres gauche et droit sont au moins de hauteur noire k-1. Par hypothèse de récurrence, ils ont chacun au moins 2k-1-1 nœuds internes et l'arbre a au moins (2k-1-1)+(2k-1-1)+1 = 2k-1 nœuds internes au total. Ceci montre que la hauteur noire k d'un arbre vérifie k ≤ ln(n+1). Puisque la racine peut être supposée noire et qu'une branche ne contient pas deux nœuds rouges consécutifs, la hauteur h de l'arbre vérifie h ≤ 2k. Elle vérifie donc finalement h ≤ 2ln(n+1).
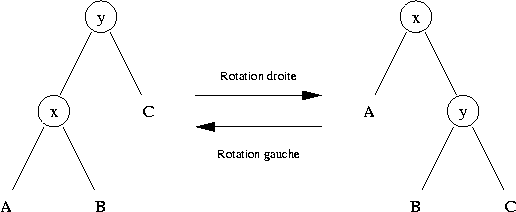
Les rotations sont des modifications locales d'un arbre binaire. Elles consistent à échanger un nœud avec l'un de ses fils. Dans la rotation droite, un nœud devient le fils droit du nœud qui était son fils gauche. Dans la rotation gauche, un nœud devient le fils gauche du nœud qui était son fils droit. Les rotations gauche et droite sont inverses l'une de l'autre. Elle sont illustrées à la figure ci-dessous. Dans les figures, les lettres majuscules comme A, B et C désignent des sous-arbres.
L'insertion d'une valeur dans un arbre rouge et noire commence par l'insertion usuelle d'une valeur dans un arbre binaire de recherche. Le nouveau nœud devient rouge de telle sorte que la propriété (3) reste vérifiée. Par contre, la propriété (2) n'est plus nécessairement vérifiée. Si le père du nouveau nœud est également rouge, la propriété (2) est violée.
Afin de rétablir la propriété (2), l'algorithme effectue des modifications dans l'arbre à l'aide de rotations. Ces modifications ont pour but de rééquilibrer l'arbre.
Soit x le nœud et p son père qui sont tous les deux rouges. L'algorithme distingue plusieurs cas.
Comme pour l'insertion d'une valeur, la suppression d'une valeur dans un arbre rouge et noir commence par supprimer un nœud comme dans un arbre binaire de recherche. Si le nœud qui porte la valeur à supprimer a zéro ou un fils, c'est ce nœud qui supprimer et son éventuel fils prend sa place. Si au contraire, ce nœud a deux fils, il n'est pas supprimé. La valeur qu'il porte est remplacée par la valeur suivante dans l'ordre et c'est le nœud qui portait cette valeur suivante qui est supprimé. Ce nœud supprimé est le nœud au bout de la branche gauche du sous-arbre droit du nœud qui portait la valeur à supprimer. Ce nœud n'a pas de fils gauche.
Si le nœud supprimé est rouge, la propriété (3) reste vérifiée. Si le nœud supprimé est noir, on considère que le nœud qui remplace le nœud supprimé porte une couleur noire en plus. Ceci signifie qu'il devient noir s'il est rouge et qu'il devient doublement noir s'il est déjà noir. La propriété (3) reste ainsi vérifié mais il y a éventuellement un nœud qui est doublement noir.
Afin de supprimer ce nœud doublement noir, l'algorithme effectue des modifications dans l'arbre à l'aide de rotation. Soit x le nœud doublement noir.
On présente ici une implémentation simpliste des arbres rouges et noirs. Comme les manipulations sur les arbres rouges et noirs utilisent comme les arbres AVL des rotations, l'implémentation tire partie de la programmation objet pour factoriser l'implémentation de ces deux types d'arbres. Les classes données ci-dessous se répartissent en trois catégories : les classes spécifiques aux arbres rouges et noirs, les classes spécifiques aux arbres AVL et les classes implémentant des parties communes.