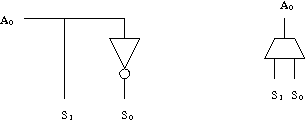
Schéma et symbole d'un décodeur 1 bit
Les décodeurs et multiplexeurs sont des circuits relativement élémentaires mais très souvent utilisés. Il s'agit de deux briques de base pour la construction de circuits plus élaborés. Ils sont en particulier présents dans chaque circuit mémoire. Un décodeur y décode l'adresse et active la ligne correspondante. Un multiplexeur permet d'y sélectionner la bonne sortie lors d'une lecture.
Un décodeur k bits possède k entrées et 2k sorties. La sortie dont le numéro est donné par les entrées est active (valeur 1) alors que toutes les autres sorties sont inactives (valeur 0).
Le décodeur 1 bit a donc une seule entrée A0 et deux sorties S0 et S1. La table de vérité des sorties S0 et S1 est la suivante.
| Entrée | Sorties | |
|---|---|---|
| A0 | S0 | S1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
On remarque que la sortie S0 est la négation de l'entrée A0 alors que la sortie S1 est égale à A0. On a donc le circuit suivant avec un seul inverseur.

Schéma et symbole d'un décodeur 1 bit
Le décodeur 2 bits a deux entrées A0 et A1 ainsi que quatre sorties S0, S1, S2 et S3. La table de vérité des quatre sorties en fonction des deux entrées est la suivante.
| Entrées | Sorties | ||||
|---|---|---|---|---|---|
| A1 | A0 | S0 | S1 | S2 | S3 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
On remarque que l'on a les quatre formules suivantes pour les sorties.
S0 = ¬A1 ∧ ¬A0
S1 = ¬A1 ∧ A0
S2 = A1 ∧ ¬A0
S3 = A1 ∧ A0
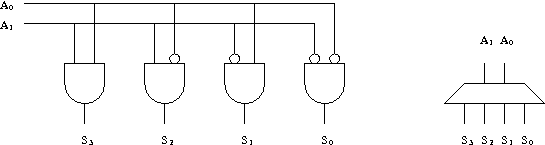
Schéma et symbole d'un décodeur 2 bits
Le décodeur 3 bits a 3 entrées et 8 sorties. Chaque sortie est obtenue comme le et logique des entrées ou de leurs négations. Les entrées devant être inversées correspondent aux zéros dans l'écriture en binaire du numéro de la sortie. Ainsi la sortie S5 est égal à A2 ∧ ¬A1 ∧ A0 car 5 s'écrit 101 en binaire.
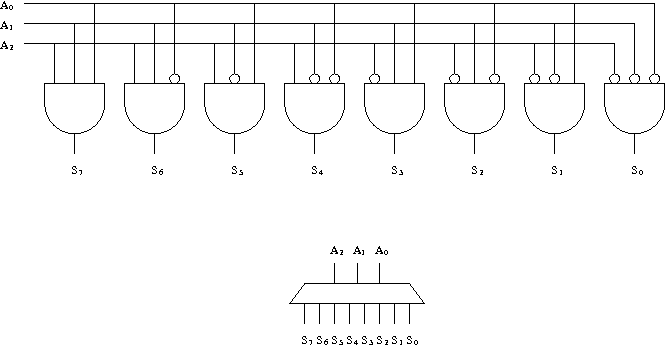
Schéma et symbole d'un décodeur 3 bits
Les circuits donnés pour k égal à 1, 2 et 3 se généralisent facilement à un entier quelconque. Le circuit est alors constitué d'inverseurs et de 2k portes and ayant chacune k entrées. Le nombre d'inverseurs nécessaires est k puisqu'il en faut un pour chaque entrée Ai afin de disposer de sa négation ¬Ai. Sur les schémas pour k = 1, 2, 3, certains inverseurs peuvent être évités en réutilisant une valeur calculée par un autre. Par contre, les schémas deviennent beaucoup moins clair. Comme chaque porte and à k entrées peut être réalisée avec k-1 portes and à 2 entrées (cf. la section portes logiques), on obtient un total de (k-1)2k portes and. La profondeur de ce circuit est alors ⌈log2(k)⌉.
Il est possible de construire de manière récursive un décodeur ayant n entrée. Il faut alors introduire un circuit un peu plus général avec une nouvelle entrée appelée CS pour Chip Select. Un décodeur k bits avec une entrée CS possèdent donc k+1 entrées CS, A0, …, Ak-1 et 2k sorties S0, …, S2k-1. Ce circuit se comporte de la façon suivante. Si l'entrée CS vaut 0, toutes les sorties valent 0 et si CS vaut 1, il se comporte comme un simple décodeur. L'entrée dont le numéro s'écrit en binaire Ak-1 … A0 vaut 1 et toutes les autres sorties valent 0.
Pour k = 1, la table de vérité du décodeur 1 bit avec une entrée CS est donc la suivante.
| Entrée | Sorties | ||
|---|---|---|---|
| CS | A0 | S0 | S1 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
On en déduit facilement le circuit ci-dessous.
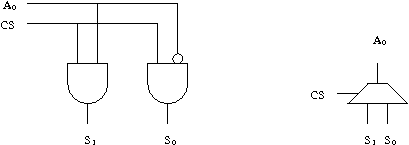
Schéma et symbole d'un décodeur 1 bit avec entrée CS
Pour k > 1, on peut construire un décodeur à k+1 entrées en utilisant deux décodeurs à k entrées et un décodeur à 1 entrée et en les combinant comme sur le schéma ci-dessous. Les deux décodeurs à k entrées reçoivent les entrées A0, …, Ak-1 et leurs deux entrées CS sont commandées par les deux sorties du décodeur 1 bit. Ce dernier reçoit en entrée Ak et CS.
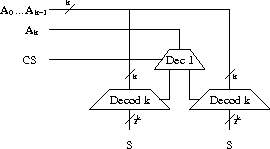
Construction récursive d'un décodeur à k+1 entrées
Pour k égal à 2 et 3, la construction donne les deux décodeurs suivants.
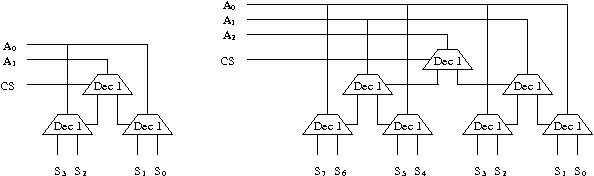
Schémas des décodeurs récursifs 2 et 3 bits
On montre facilement que le nombre de décodeurs 1 bit utilisés dans le décodeur k bits est 2k-1 et que le nombre de portes and utilisées est donc 2k+1-2. La profondeur du circuit est k. Par rapport au décodeur construit de manière directe, le circuit construit récursivement utilise moins de portes logiques (2k+1 au lieu de k2k) mais a une profondeur supérieure (k au lieu de ⌈log2(k)⌉).
Un multiplexeur est en quelque sorte l'inverse d'un décodeur. Un multiplexeurs k bits permet de sélectionner une entrée parmi 2k disponibles. Un multiplexeur k bits a k + 2k entrées et une seule sortie. Les k premières entrées A0,…,Ak-1 sont appelées bits d'adresses car elles donnent le numéro de l'entrée à sélectionner parmi les entrées B0,…,B2k-1. La sortie S est alors égale à cette entrée sélectionnée.
Le multiplexeur 1 bit a donc 3 entrées A0, B0 et B1 et une seule sortie S. La formule donnant la sortie S en fonction des entrées est la suivante.
S = (A0 ∧ B1) ∨ (¬A0 ∧ B0)
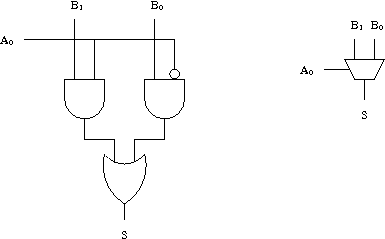
Schéma et symbole d'un multiplexeur 1 bit
Le multiplexeur 2 bit a donc 6 entrées A0, A1, B0, B1, B2 et B3 et une seule sortie S. La formule donnant la sortie S en fonction des entrées est la suivante.
S = (A1 ∧ A0 ∧ B3) ∨ (A1 ∧ ¬A0 ∧ B2) ∨ (¬A1 ∧A0 ∧ B1) ∨ (¬A1 ∧¬A0 ∧ B0)
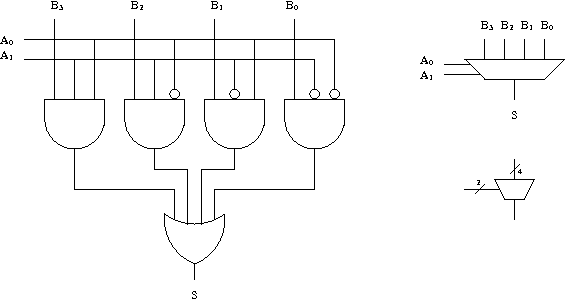
Schéma et symbole d'un multiplexeur 2 bits
Le multiplexeur k bits peut être construit récursivement en utilisant le schéma ci-dessous qui donne la construction d'un multiplexeur k+1 bits avec deux multiplexeurs k bits et un multiplexeur 1 bit.
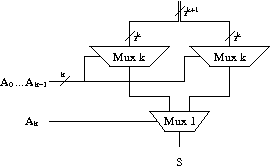
Multiplexeur k+1 bits construit avec deux multiplexeurs k bits
Pour k égal à 2 et 3, la construction donne les deux multiplexeurs suivants.
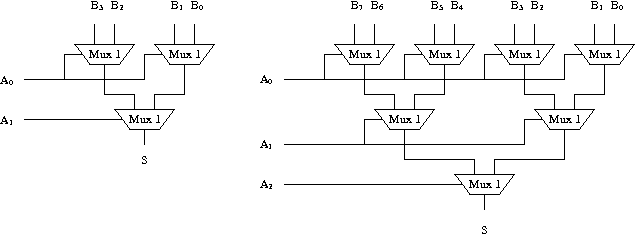
Schémas des multiplexeurs récursifs 2 et 3 bits
Comme pour les décodeurs récursifs, on montre facilement que le nombre de multiplexeurs 1 bit utilisés dans le multiplexeur k bits est 2k-1 et que le nombre de portes logiques and et or utilisées est donc 3(2k-1). La profondeur du circuit est k. Par rapport au multiplexeur construit de manière directe, le circuit construit récursivement utilise moins de portes logiques (3 2k au lieu de k2k) mais a une profondeur supérieure (k au lieu de ⌈log2(k)⌉).
Dans cette partie, nous expliquons comment construire le circuit d'une fonction booléenne. Nous allons le faire sur l'exemple de la fonction hidden bit.
Nous commençons par donner la définition de la fonction hidden bit. Cette fonction prend en entrée k valeurs booléennes et retourne une valeur booléenne. Soient k entrées binaires A1,…, Ak et soit s la somme de ces entrées, c'est-à-dire le nombre d'entrées égales à 1 : s = #{ i | Ai = 1 }. Cette somme est comprise entre 0 et k. La sortie S est alors égale à 0 si s = 0 et elle est égale à As si 1 ≤ s ≤ k.
| Entrée | Sorties | |
|---|---|---|
| A1 | s | S |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
On a alors l'égalité S = A1. Le circuit est dans ce cas trivial puisqu'il se contente de mettre l'entrée A1 en sortie.
| Entrées | Sorties | ||
|---|---|---|---|
| A1 | A2 | s | S |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 2 | 1 |
On a alors l'égalité S = A1. Le circuit est encore une fois immédiat puisqu'il se contente de mettre l'entrée A1 en sortie.
Le cas k = 3 est le premier cas intéressant. On commence par calculer la table qui donne pour chaque valeur des entrées les valeurs des deux sorties s et S.
| Entrées | Sorties | |||
|---|---|---|---|---|
| A1 | A2 | A3 | s | S |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 2 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 2 | 0 |
| 0 | 1 | 1 | 2 | 1 |
| 1 | 1 | 1 | 3 | 1 |
À Partir de cette table de vérité de la fonction, il est facile de trouver une expression de la sortie S en fonction des trois entrées A1, A2 et A3.
S = A1 A2 A3 + A1 A2 A3 + A1 A2 A3 + A1 A2 A3
Les quatre monômes correspondent aux quatre lignes de la table où la sortie prend la valeur 1. Le premier monôme A1A2A3 correspond par exemple à la seconde ligne de la table. La sortie S vaut 1 lorsque A1 = 1, A2 = 0 et A3 = 0.
Il est possible de construire un circuit à partir de la formule ci-dessus. Les valeurs des monômes peuvent être calculées par quatre portes et à trois entrées et la valeur finale de S peut être calculée par trois portes ou à deux entrées. Afin de construire un circuit le plus petit possible, il est nécessaire de simplifier au maximum la formule.
La formule ci-dessus peut être simplifiée. La somme des deux premiers monômes peut être réduite à un seul monôme plus simple de la façon suivante.
A1 A2 A3 + A1 A2 A3 = A1 A3 (A2 + A2) = A1 A3
Nous présentons maintenant une méthode graphique élémentaire permettant de trouver une expression simple pour une formule. Cette méthode dite des tables de Karnaugh (cf. aussi wikibook) ne donne pas toujours la meilleure expression mais elle fonctionne relativement bien tout en étant facile à mettre en œuvre.
Nous expliquons la méthode sur notre exemple. La méthode consiste à disposer les valeurs de l'expression dans une table rectangulaire comme ci-dessous.
| A1 | A1 | |||
|---|---|---|---|---|
| A2 | A2 | A2 | A2 | |
| A3 | 1 | 0 | 0 | 1 |
| A3 | 1 | 1 | 0 | 0 |
Il faut essayer alors de regrouper les valeurs 1 en blocs rectangulaires. Ainsi, les deux 1 rouges correspondent à A1 = 1 et A3 = 0. Ils donnent donc le monôme A1A3 que nous avions obtenu en regroupant les deux premiers monômes de notre formule initiale. Les blocs de 1 peuvent ne pas être contigus. Les deux 1 bleus correspondent à A2 = 1 et A3 = 1 et ils donnent le monôme A2A3. Les blocs de 1 peuvent éventuellement se chevaucher. On a donc finalement trouvé la formule suivante pour S.
S = A2 A3 + A1 A3
Le circuit construit à partir de la formule précédente ne contient plus que deux portes et et une porte ou à deux entrées. On reconnaît le circuit d'un multiplexeur 1 bit où A3 est le bit d'adresse (ou de commande) et A1 et A2 sont les entrées.
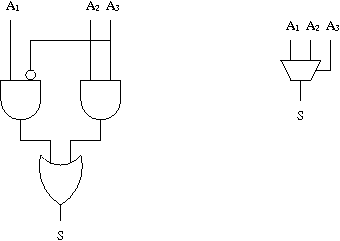
Schéma pour la fonction hidden bit à 3 entrées
| Entrées | Sorties | ||||
|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | s | S |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 2 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 2 | 0 |
| 0 | 1 | 1 | 0 | 2 | 1 |
| 1 | 1 | 1 | 0 | 3 | 1 |
| 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 2 | 0 |
| 0 | 1 | 0 | 1 | 2 | 1 |
| 1 | 1 | 0 | 1 | 3 | 0 |
| 0 | 0 | 1 | 1 | 2 | 0 |
| 1 | 0 | 1 | 1 | 3 | 1 |
| 0 | 1 | 1 | 1 | 3 | 1 |
| 1 | 1 | 1 | 1 | 4 | 1 |
| A1 | A1 | ||||
|---|---|---|---|---|---|
| A2 | A2 | A2 | A2 | ||
| A3 | A4 | 1 | 1 | 0 | 1 |
| A4 | 1 | 0 | 0 | 1 | |
| A3 | A4 | 1 | 1 | 0 | 0 |
| A4 | 0 | 0 | 0 | 1 | |
S = A1 A3 A4 + A2 A3 A4 + A1 A2 A4 + A1 A3 A4
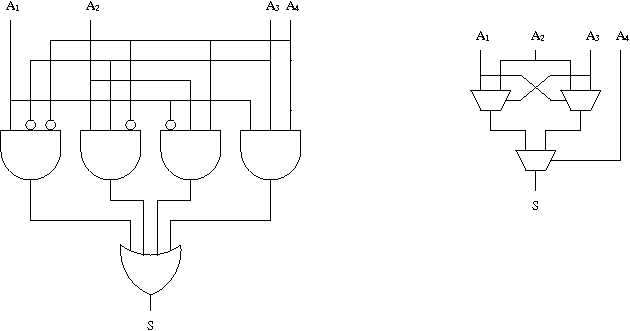
Schéma pour la fonction hidden bit à 4 entrées
S = A1
A3
A4
A5
+ A2
A3
A4
A5
+ A1
A2
A4
A5
+ A1
A3
A4
A5
+ A1
A2
A4
A5
+ A1
A3
A4
A5
+ A1
A2
A3
A5
+ A1
A2
A4
A5
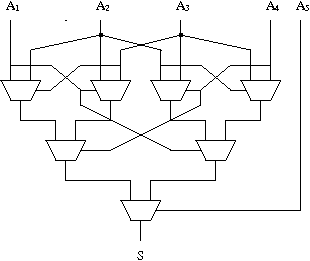
Schéma pour la fonction hidden bit à 5 entrées