Fig. 1 : graphe associé à la formule φ
On s'intéresse ici à la complexité des problèmes c'est-à-dire aux ressources nécessaires pour les résoudre. Les ressources essentielles sont le temps et l'espace. On ne considère ici que des problèmes décidables. On suppose donc que toutes les machines de Turing considérées s'arrêtent toujours. On commence par étudier le temps de calcul des machines de Turing.
Soit M une machine de Turing (a priori non déterministe) et soit w un mot sur l'alphabet d'entrée de M. On suppose que la machine M n'a pas de calcul infini. La longueur d'un calcul de M sur w est le nombre d'étape de calcul pour atteindre une configuration bloquante. Le temps de calcul tM(w) de la machine M sur l'entrée est la longueur du plus long calcul ayant w comme entrée. Si la machine M est déterministe, il n'y a qu'un seul calcul d'entrée w et le temps tM(w) est la longueur de cet unique calcul. Si la machine est non déterministe, le temps de calcul prend en compte le cas le pire, c'est-à-dire le calcul le plus long.
En fait, on s'intéresse moins au temps de calcul sur une entrée fixée qu'au comportement de la machine pour une taille d'entrée donnée. On définit la fonction de complexité en temps tM de M de la manière suivante.
tM(n) = max|w|=n tM(w).
La valeur tM(n) représente la longueur du plus long calcul de M avec une entrée de taille n. C'est encore une fois le cas le pire qui est considéré. L'essentiel n'est pas la valeur de tM(n) pour des valeurs précises de n mais le comportement de la fonction tM lorsque n devient grand. On s'intéresse plus au comportement asymptotique de tM qu'à des valeurs particulières.
Pour comparer les comportements asymptotiques des fonctions, on utilise la notation O (grand O). Soit t une fonction de N dans R+. On dit qu'une machine M décide un langage L (et par extension un problème codé par L) en temps t(n) si L est le langage accepté par M et si la fonction de complexité de M vérifie tM = O(t).
Dans la suite, on s'intéresse à la complexité d'un problème à une constante près. En effet, les comportement asymptotiques des fonctions sont comparés à l'aide de la notation O. Ce choix est motivé par le résultat suivant qui dit qu'on peut toujours diviser le temps de calcul par une constante.
Proposition. Soit f une fonction de N dans R+ telle que n = O(t(n)) et soit M une machine de Turing en temps t(n). Pour tout constante k, il existe une machine de Turing M' équivalente à M et en temps t(n)/k.
On a vu que les différentes variantes de machines de Turing sont équivalentes dans le sens où toute machine d'un modèle peut être simulée par une machine d'un autre modèle. Par contre ces simulations ont une incidence sur les temps de calcul. On étudie ici le coût du passage d'un modèle à un autre.
On a montré que toute machine à plusieurs bandes peut être simulée par une machine à une seule bande. L'idée de la simulation consiste à regrouper toutes les bandes en une seule bande. Pour simuler une seule transition de la machine à plusieurs bandes, la machine à une bande doit parcourir entièrement toute la bande. Comme le nombre de cellules de la bande contenant un symbole différent du symbole blanc est borné par le temps de calcul de la machine, on obtient le résultat suivant.
Proposition. Soit t une fonction de N dans R+ telle que t(n) ⩾ n pour tout n ⩾ 0. Une machine à plusieurs bandes qui fonctionne en temps t(n) est équivalente à une machine à une seule bande qui fonctionne en temps t2(n).
On a également montré que toute machine non déterministe peut être simulée par une machine déterministe. La simulation consiste alors à essayer successivement tous les calculs de la machine non déterministe. Si la machine non déterministe fonctionne en temps t(n), le nombre de calculs possibles pour une entrée de taille n est borné par kt(n) où k est le nombre maximal de transitions qui peuvent être effectuées à partir d'une configuration. L'entier k est le cardinal maximal des ensembles δ(p, a) = { (q, b, x) | p, a → q, b, x ∈ E } pour tout p et tout a. La temps de simulation d'un calcul est proportionnel à la longueur de ce calcul. Le temps nécessaire pour simuler tous les calculs est donc de l'ordre de t(n)kt(n). Comme on a la relation t(n)kt(n) = 2O(t(n)) si t(n) ⩾ n, on obtient le résultat suivant.
Proposition. Soit t une fonction de N dans R+ telle que t(n) ⩾ n pour tout n ⩾ 0. Une machine non déterministe qui fonctionne en temps t(n) est équivalente à une machine déterministe qui fonctionne en temps 2O(t(n)).
Pour les complexité en temps, on distingue les machines déterministes des machines non déterministes. Soit t une fonction de N dans R+. Pour les machines déterministes, on définit la classe TIME(t(n)) des problèmes qui peuvent être résolus en temps t(n).
TIME(t(n)) = { L | L peut être décidé en temps t(n) par une machine de Turing déterministe }
Pour les machines non déterministes, on définit la classe NTIME(t(n)) des problèmes qui peuvent être résolus en temps t(n).
NTIME(t(n)) = { L | L peut être décidé en temps t(n) par une machine de Turing }
La classe importante est celle des problèmes qui peuvent être résolus en temps polynomial par une machine déterministe. On définit la classe P de la manière suivante.
P = ⋃k⩾0 TIME(nk)
De manière analogue, on définit la classe des problèmes qui peuvent être résolus en temps polynomial par une machine non déterministe.
NP = ⋃k⩾0 NTIME(nk)
On a bien sûr l'inclusion triviale P ⊆ NP. Le problème de savoir s'il y a égalité ou non est un problème ouvert extrêmement difficile.
On considère aussi la classe EXPTIME des problèmes qui peuvent être résolus en temps exponentiel par une machine déterministe.
EXPTIME = ⋃k⩾0 TIME(2nk)
Les relations entre les différents modèles de machines montrent qu'on a les inclusions suivantes.
P ⊆ NP ⊆ EXPTIME
Le problème d'accessibilité dans un graphe orienté est de savoir si un graphe G donné contient un chemin de s à t pour deux sommets s et t également donnés.
L = { ⟨G, s, t⟩ | G contient un chemin de s à t }
Ce problème peut être résolu par un parcours en largeur du graphe qui s'effectue en temps linéaire dans un langage de programmation classique. Le langage L peut donc être décidé en temps polynomial par une machine de Turing déterministe. Le problème d'accessibilité appartient par conséquent à la classe P.
Une clique de taille k d'un graphe non orienté G = (V, E) est un sous-ensemble { v1, …, vk } de sommets de G tels que toutes les arêtes (vi, vj) pour tout 1 ⩽ i < j ⩽ k sont présentes dans G.
Le problème CLIQUE est de savoir si un graphe G donné contient une clique d'une taille k également donnée. Ce problème est donc codé par le langage suivant.
L = { ⟨G, k⟩ | G possède une clique de taille k }
Un algorithme non déterministe pour décider ce langage L peut fonctionner de la manière suivante. L'algorithme commence par choisir de façon non déterministe k sommets v1, …, vk de G. Ce choix se fait en temps linéaire en la taille du graphe. Ensuite, l'algorithme vérifie que les toutes les arêtes (vi, vj) pour tout 1 ⩽ i < j ⩽ k sont présentes dans G et il accepte si c'est le cas. Cette vérification peut se faire en temps polynomial puiqu'il y a de l'ordre de k2 arêtes à tester. Cet algorithme décide si le graphe G possède une clique de taille k. En effet, il y a un calcul de l'algorithme pour chaque choix possible de k sommets. Un de ces calculs est acceptant si G contient une clique. Le problème de la clique appartient donc à la classe NP.
On introduit ici le problème SAT de satisfiabilité d'une formule et sa variante 3-SAT.
Une formule est formée à partir de variables booléennes en utilisant les trois opérateurs de négation (noté par le symbole ¬), du et logique (noté par le symbole ∧) et du ou logique (noté par le symbole ∨). Par exemple, la formule φ = (x ∨ ¬y ∨ z) ∧ (¬x ∨ t) utilise les quatre variables x, y, z, et t.
Un littéral est soit une variable soit la négation d'une variable comme x ou ¬x. La négation d'une variable x est souvent notée en mettant une barre au dessus de la variable. Une clause est la disjonction (c'est-à-dire le ou) de un ou plusieurs littéraux comme x ∨ ¬y ∨ z. Une formule est dite en forme normale conjonctive si elle est la conjonction (c'est-à-dire le et) de une ou plusieurs clauses comme la formule φ ci-dessus.
Une formule est dite satisfiable s'il est possible d'affecter une valeur vrai (noté 1) ou faux (noté 0) à chacune des variables de telle façon que la formule ait la valeur vrai. La formule φ ci-dessus est satisfiable car elle prend la valeur 1 lorsqu'on affecte les valeurs x = 1, y = 0, z = 0 et t = 1, par exemple. Par contre la formule x ∧ ¬x ∧ y n'est pas satisfiable.
Le problème de satisfiabilité SAT est de savoir si une formule donnée est satisfiable. Le problème de satisfiabilité 3-SAT est de savoir si une formule donnée en forme normale conjonctive avec trois littéraux par clause est satisfiable. Le problème 3-SAT est donc un cas particulier de SAT.
Une instance du problème 3-SAT est une formule de la forme
φ = (a1 ∨ b1 ∨ c1) ∧ (a2 ∨ b2 ∨ c2) ∧ … ∧ (ak ∨ bk ∨ ck)
où chacun des ai, bi et ci est un littéral xj ou ¬xj pour une variable xj.
Les problèmes SAT et 3-SAT sont décidés par l'algorithme non déterministe suivant. L'algorithme commence par choisir de façon non déterministe la valeur affectée à chacune des variables. Ensuite l'algorithme calcule la valeur de la formule et vérifie que cette valeur est bien 1. Ce calcul de la valeur se fait bien sûr en temps linéaire. Les problèmes SAT et 3-SAT sont donc dans la classe NP.
Les deux algorithmes ci-dessus pour le problème de la clique et le problème de satisfiabilité d'une formule ont la même structure. Ils sont tous les deux formés de deux parties. Dans une première partie, l'algorithme choisit de façon on déterministe un objet et dans une seconde partie, il vérifie que cet objet satisfait une certaine propriété. Pour le problème de la clique, l'objet choisi est un sous-ensemble de sommets et il est vérifié que ce sous-ensemble de sommets constitue effectivement une clique. Pour le problème de satisfiabilité, l'objet choisi est une affectation aux variables et il est vérifié que cette affectation donne la valeur vrai à la formule. Dans les deux cas, la vérification se fait en temps polynomial. Ceci est un principe général. Tout problème de la classe NP est équivalent à un problème de vérification en temps polynomial.
Un vérificateur en temps polynomial pour un langage L est une machine de Turing V déterministe qui prend des entrées de la forme ⟨w, c⟩ avec un temps de calcul polynomial en la taille de w et tel que :
L = { w | ∃ c tel que V accepte ⟨w, c⟩ }
On a la proposition suivante qui établit que les problèmes de la classe NP sont ceux qu'on peut vérifier en temps polynomial.
Proposition. Un langage L est dans la classe NP si et seulement si il existe un vérificateur en temps polynomial pour L.
S'il existe un vérificateur V pour L, on peut construire, de la manière suivante une machine M non déterministe qui décide L et qui fonctionne en temps polynomial. La machine commence par choisir de façon non déterministe c puis simule le vérificateur V sur ⟨w, c⟩ pour vérifier que V accepte cette entrée. Puisque V fonctionne en temps polynomial, c doit être de taille polynomiale et donc tout le calcul de M se fait en temps polynomial.
Réciproquement, supposons que la machine M non déterministe décide le langage L. On associe à chaque w, la suite c des transitions effectuées par la machine M pour accepter w. Par définition, cette suite est de longueur polynomiale. Le vérificateur V simule la machine M sur w le long du calcul c pour vérifier que c'est effectivement un calcul acceptant w. Cette vérification se fait en temps proportionnel à c et donc en temps polynomial.
Dans le cadre des problèmes décidables, une réduction permet de ramener la décidabilité d'un problème à celle d'un autre problème. On introduit des réductions qui prennent en compte le temps de calcul de la fonction qui fait passer d'un problème A à un autre problème B. Une réduction polynomiale fait correspondre à une instance du problème A une instance du problème B qui a la même réponse et qui est calculable en temps polynomial.
On suppose que les problèmes A et B sont codés par les langages LA et LB sur des alphabets ΣA et ΣB. Une réduction polynomiale de A à B est une fonction f de ΣA* dans ΣB* calculable en temps polynomial par une machine de Turing telle que
w ∈ LA ⇔ f(w) ∈ LB
On note A ⩽P B lorsqu'il existe une réduction polynomiale du problème A au problème B.
Pour illustrer la notion de réduction polynomiale, nous allons montrer une réduction du problème 3-SAT au problème CLIQUE. Soit φ une instance de 3-SAT, c'est-à-dire une formule en forme conjonctive telle que chaque clause de φ contienne trois littéraux.
φ = (l1 ∨ l2 ∨ l3) ∧ (l4 ∨ l5 ∨ l6) ∧ … ∧ (l3k-2 ∨ l3k-1 ∨ l3k)
On introduit alors le graphe non orienté G dont l'ensemble des sommets est l'ensemble V = { l1, …, l3k } de tous les littéraux de φ. Deux sommets de G sont reliés par une arête s'ils n'appartiennent pas à la même clause et s'ils ne sont pas contradictoires. Par non contradictoire, on entend que l'un n'est pas égal à la négation de l'autre. L'ensemble E des arêtes est donc défini de la manière suivante.
E = { (li, lj) | ⌊(i-1)/3⌋ ≠ ⌊(j-1)/3⌋ et li ≠ ¬lj }
En effet, le numéro de la clause d'un littéral li est égal à ⌊(i-1)/3⌋ si les clauses sont numérotées à partir de 0.
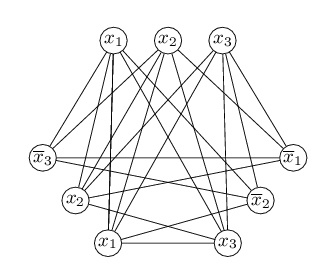
Pour la formule φ = (x1 ∨ x2 ∨ x3) ∧ (¬x1 ∨ ¬x2 ∨ x3) ∧ (x1 ∨ x2 ∨ ¬x3), on obtient le graphe représenté à la figure ci-dessous.

Fig. 1 : graphe associé à la formule φ
Nous allons voir que la formule φ est satisfiable si et seulement si le graphe G contient une clique de taille k. On remarque que deux littéraux d'une même clause ne sont jamais reliés par une arête. Une clique peut donc contenir au plus un littéral par clause et elle est de taille au plus k.
Supposons d'abord que la formule φ est satisfiable. Il existe donc une affectation des variables telle que φ vaille 1. Ceci signifie qu'au moins un littéral par clause vaut la valeur 1. Choisissons un tel littéral dans chacune des clauses pour former un ensemble de k littéraux. Comme tous ces littéraux valent 1, deux d'entre eux ne peuvent pas être contradictoires et ils sont donc reliés par des arêtes. C'est donc une clique de taille k dans G.
Supposons maintenant que G contienne une clique de taille k. Comme les littéraux d'une même clause ne sont pas reliés, cette clique contient un littéral exactement dans chaque clause. Montrons alors qu'il existe une affectation qui rend tous ces littéraux égaux à 1. Chaque littéral de cette clique est égal à xi ou à ¬xi. Pour que ce littéral vaille 1, on impose la valeur 1 ou 0 à la variable correspondante xi. Comme tous les littéraux de la clique sont reliés par une arête, ils ne sont pas contradictoires deux à deux. Ceci signifie que deux littéraux quelconques de la clique concernent deux variables distinctes xi et xj avec i ≠ j ou alors ils concernent la même variable xi mais ils imposent la même valeur à la variable xi. On obtient alors une affectation cohérente des variables apparaissant dans la clique. En affectant n'importe quelle valeur à chacune des autres variables, on obtient une affectation qui donne la valeur 1 à la formule φ.
De manière intuitive, un problème est NP-complet s'il est parmi les problèmes les plus difficiles de la classe NP. Plus formellement un problème A est dit NP-complet si les deux conditions suivantes sont remplies.
Si seule la seconde condition est vérifiée, on dit que le problème A est NP-difficile.
L'intérêt des problèmes NP-complets est double. D'un point de vue théorique, ces problèmes sont des candidats potentiels pour être des problèmes de la classe NP qui ne sont pas dans P si NP est différent de P. En effet, il suffit qu'un seul problème NP-complet soit dans P pour qu'on ait l'égalité P = NP. D'une point de vue pratique, le fait qu'un problème est NP-complet montre qu'il est utopique de chercher un algorithme polynomial résolvant ce problème puisque cet algorithme résoudrait du même coup des centaines d'autres d'autres problèmes qui ont fait l'objet de recherches intensives.
Un résultat important est qu'il existe effectivement des problèmes qui sont NP-complets. Le résultat suivant est dû à Cook et Levin.
Théorème (Cook et Levin). Les problèmes SAT et 3-SAT sont NP-complets.
Il a déjà été vu que les deux problèmes SAT et 3-SAT sont dans la classe NP. Pour montrer qu'ils sont en outre NP-complets, il reste à montrer que tout problème de la classe NP se réduit polynomialement à SAT et à 3-SAT. Dans une première étape, on réduit un problème quelconque de NP à SAT. Ceci montre que SAT est NP-complet. Dans une seconde étape, on réduit SAT à 3-SAT. En composant les deux réductions, on obtient que 3-SAT est également NP-complet.
Soit A un problème de la classe NP. Il est donc accepté par une machine de Turing M a priori non déterministe. Nous allons montrer que pour toute entrée w de M, il existe une formule φw de taille polynomiale en la taille de w qui est satisfiable si et seulement si w est acceptée par M. L'idée est que la formule φw code d'une certaine manière l'existence d'une calcul acceptant de M sur l'entrée w.
On note n = |w| la taille de l'entrée w. Puisque la machine M fonctionne en temps polynomial, il un entier fixe k tel que tout calcul sur w soit de longueur au plus nk. Quitte à modifier M en ajoutant une boucle d'attente, on peut supposer que tout calcul acceptant sur w est de longueur nk exactement. Comme la machine M fonctionne en temps nk, elle utilise au plus nk cellules de la bande. Les configurations d'un calcul acceptant sont donc de longueur au plus nk. Quitte à écrire quelques symboles blancs implicites à la fin de la configuration, on peut supposer que toutes les configurations sont exactement de tailles nk. En écrivant toutes ces configurations les unes au-dessus des autres, on obtient un tableau de symboles (pris dans Γ ∪ Q) de taille nk × nk (cf. figure ci-dessous). On écrit alors une formule φw qui code l'existence d'un tel tableau de symboles formé par les configurations successives d'un calcul acceptant sur w.
| Conf. | 0 | 1 | 2 | 3 | … | nk | Espace |
|---|---|---|---|---|---|---|---|
| C0 = | q0 | w1 | w2 | w3 | … | # | |
| C1 = | w'1 | q1 | w2 | w3 | … | # | |
| C2 = | w'1 | w'2 | q2 | w3 | … | # | |
| C3 = | … | … | … | … | … | # | |
| … | … | … | … | … | … | … | |
| Cnk | … | … | … | … | … | … |
Pour chaque case (i, j) du tableau avec 0 ⩽ i, j ⩽ nk et pour chaque symbole a de l'alphabet A = Γ ∪ Q, on introduit une variable xi, j, a qui code le fait que la case (i, j) du tableau contienne ou non le symbole a. Le nombre de ces variables |A| × n2k qui est bien polynomial en n.
La formule φw se décompose en la conjonction φcell ∧ φstart ∧ φmove ∧ φaccept où chacune des quatre formules φcell, φstart, φmove et φaccept code un des aspects de l'existence d'un chemin acceptant. La formule φcell code le fait que chaque cellule du tableau contient un et un seul symbole de A. Ceci signifie que pour chaque i et j fixés une seule des variables xi, j, a reçoit la valeur 1. La formule φstart code le fait que la première ligne du tableau est bien la configuration initiale q0w. La formule φmove code le fait que chaque ligne du tableau est obtenue à partir de la précédente en appliquant une des transitions de la machine M. Cette formule assure que le tableau est bien issu d'un calcul. La dernière formule φaccept code le fait que ce calcul est acceptant, c'est-à-dire que l'état de la dernière configuration est acceptant. La seule formule délicate à écrire est la formule φmove.
La formule φcell est la conjonction d'une formule pour chaque cellule (i, j). Cette dernière garantit qu'au moins une des variables xi, j, a a la valeur 1 mais que deux variables xi, j, a et xi, j, b pour a ≠ b ne peuvent avoir la valeur 1 simultanément. La formule φcell s'écrit de la façon suivante.
φcell = ∧0 ⩽ i, j ⩽ nk [(∨a ∈ A xi, j, a) ∧ (∧a ≠ b ¬(xi, j, a ∧ xi, j, b)) ]
La formule φstart s'écrit directement de la façon suivante.
φstart = x0, 0, q0 ∧ x0, 1, w1 ∧ x0, 2, w2 ∧ … ∧ x0, n, wn ∧ x0, n+1, # ∧ … ∧ x0, nk, #
La formule φaccept assure qu'au moins une des cases de la dernière ligne du tableau contient un état final. Elle s'écrit simplement de la façon suivante.
φaccept = ∨0 ⩽ j ⩽ nk et q ∈ F xnk, j, q
La formule φmove mérite un peu plus d'attention. Il faut remarquer que le contenu d'une case (i, j) dépend uniquement des contenus des trois cases au-dessus (i-1, j-1), (i-1, j) et (i-1, j+1) et de la transition qui a été effectuée par la machine pour passer de la configuration Ci-1 à la configuration Ci. En fait, il est seulement nécessaire de connaître la transition effectuée lorsqu'une des trois cases au-dessus contient l'état de la configuration Ci-1. Si les trois symboles contenus dans les trois cases au-dessus sont des symboles de bande, alors le symbole de la case (i, j) est identique au symbole de la case (i-1, j). Ces remarques impliquent qu'il est possible de vérifier que la ligne i est bien obtenue à partir de la ligne i-1 uniquement en regardant les contenus des fenêtres de taille 2 × 3. La machine M étant fixée, on considère tous les contenus possibles des fenêtres de taille 2 × 3. Le nombre de ces contenus possibles ne dépend que de l'alphabet et des transitions de la machine. C'est donc un nombre fixe qui ne dépend pas de n. Le fait que six cases du tableau correspondent s'écrit comme une conjonction de six variables xi, j, a. Le fait que toutes les parties de six cases du tableaux correspondent à un des contenus possibles des fenêtre s'exprime par la conjonction pour 0 ⩽ i, j ⩽ nk d'une disjonction sur les différents contenus. Ceci est une formule de taille polynomiale en n.
Nous montrons maintenant que le problème SAT se réduit polynomialement au problème 3-SAT. Nous montrons que pour toute formule quelconque φ, il existe une formule φ' en forme normale conjonctive avec trois littéraux par clause et calculable en temps polynomial telle que φ est satisfiable si et seulement si φ' est satisfiable. Le calcul de φ' se fait en trois étapes. La première étape consiste à ramener toutes les négations devant les variables pour obtenir une formule sans négation autre que dans les littéraux. La seconde étape consiste à obtenir une formule en forme normale conjonctive mais avec des clauses ayant des nombres quelconques de littéraux. La troisième et dernière étape produit finalement la formule φ' en forme normale conjonctive avec trois littéraux par clause. Les première et troisième étapes sont faciles. Par contre la deuxième étape recèle une difficulté.
La première étape fait descendre les négations à l'intérieur de la formule en utilisant les lois de De Morgan : ¬(A ∨ B) ≡ ¬A ∧ ¬B et ¬(A ∧ B) ≡ ¬A ∨ ¬B où le symbole ≡ signifie que deux formules sont équivalentes. Cette descente des négations s'arête lorsque toutes celles-ci se trouvent devant des variables. La formule obtenue est équivalent à la formule de départ. Cette transformation des formules se fait en temps linéaire si les formules sont représentées sous formes d'arbres et donc en temps polynomial sur une machine de Turing.
La formule de départ n'utilise plus de négation hormis dans les littéraux. La formule est donc uniquement constituée des opérateurs ∧ et ∨. Une première idée naïve serait d'utiliser la distributivité de chacun de ces opérateurs par rapport à l'autre pour obtenir une formule équivalente en forme normale conjonctive. Cette approche ne marche pas car la formule obtenu peut avoir une taille exponentielle en la formule de départ. La formule φ ci-dessous est un exemple pathologique.
φ = (x1 ∧ y1) ∨ (x2 ∧ y2) ∨ … ∨ (xn ∧ yn)
Si la formule φ est développée, on obtient la conjonction de tous les monômes de la forme z1 ∨ z2 ∨ … ∨ zn où chaque zi est soit xi soit yi. Comme il y a 2n monômes de cette forme, la formule développée a une taille de l'ordre n2n alors que la taille de φ est de l'ordre de n.
L'idée pour éviter ce problème est de calculer une formule φ'' qui n'est pas nécessairement équivalente à la formule de départ. Par contre la propriété d'être satisfiable reste préservée par la formule φ''. L'idée est que les affectations de la formule φ se prolongent en plusieurs affectations de la formule φ''.
Le calcul de la formule se fait par induction sur la forme de la formule φ.
φ'' = (y ∨ E1) ∧ … ∧ (y ∨ Ek) ∧ (¬y ∨ F1) ∧ … ∧ (¬y ∨ Fm)
où y est une nouvelle variable qui est introduite.Dans les deux cas, la formule φ'' est satisfiable si et seulement si la formule φ est satisfiable. On vérifie également que la taille de φ'' est au plus quadratique en la taille de φ et que φ'' se calcule effectivement en temps quadratique.
Cette dernière étape consiste à remplacer les clauses n'ayant pas trois littéraux par une ou plusieurs clauses ayant exactement trois littéraux.
Si une clause a seulement un ou deux littéraux, on peut facilement la transformer en une clause à trois littéraux en répétant plusieurs fois le même littéral. Ainsi la clause x1 ∨ x2 devient la clause x1 ∨ x2 ∨ x2 qui est bien sûr équivalente.
Si au contraire une clause a plus de trois littéraux, on effectue la transformation suivante. Supposons que la clause soit égale à la disjonction l1 ∨ … ∨ lk des k littéraux l1, …,lk. On la remplace par la conjonction suivante de k-2 clauses à trois littéraux.
(l1 ∨ l2 ∨ y1) ∧ (¬y1 ∨ l3 ∨ y2) ∧ (¬y2 ∨ l4 ∨ y3) ∧ … ∧ (¬yk-4 ∨ lk-2 ∨ yk-3) ∧ (¬yk-3 ∨ lk-1 ∨ lk)
où les variables y1, …,yk-3 sont nouvellement introduites. On vérifie que toute affectation qui rend vraie la clause l1 ∨ … ∨ lk se prolonge en une affectation aux variables y1, …,yk-3 qui rend vraie la conjonction. Réciproquement, toute affectation qui rend vraie la conjonction rend vraie la clause initiale. Cette dernière tranformation se fait en temps linéaire en la taille de la formule et donc en temps polynomial sur une machine de Turing.
Pour montrer qu'un problème A est NP-complet, if faut d'abord montrer qu'il est dans la classe NP et qu'ensuite tout autre problème B de NP se réduit polynomialement à A. Pour la seconde partie, il n'est pas nécessaire de le faire pour tous les problèmes B de NP. Il suffit en effet de montrer qu'un seul problème B qui est NP-complet se réduit à A. On a en effet la proposition suivante.
Proposition. Si B est NP-complet et si B ⩽P A, alors A est NP-difficile.
Puisque B est NP-complet, on a C ⩽P B pour tout problème C de NP. Si on a aussi B ⩽P A, on obtient C ⩽P A en combinant les deux relations.
Grâce à la proposition précédente, montrer qu'un problème A est NP-complet consiste à montrer qu'il est dans la classe NP et ensuite à montrer qu'un problème B qu'on sait être déjà NP-complet se réduit à A. Nous allons appliquer cette technique à plusieurs problèmes classiques.
Nous avons déjà vu que CLIQUE est dans la classe NP. Nous avons aussi montré que le problème 3-SAT se réduit polynomialement au problème CLIQUE. Il découle de la proposition précédente que le problème CLIQUE est NP-complet.
Une arête (u, v) d'un graphe est dite adjacente à un sommet s si s est égal à u ou à v. Une couverture de taille k d'un graphe G = (V, E) est un sous-ensemble C de k sommets tel que toute arête de G est adjacente à au moins un des sommets de C.
Le problème de la couverture (appelé VERTEX-COVER) est de savoir si un graphe G donné contient une couverture d'une taille k également donnée.
Proposition. Le problème VERTEX-COVER est NP-complet.
Le problème VERTEX-COVER est dans NP. Un algorithme pour résoudre ce problème commence par choisir de façon non déterministe les k sommets u1, …, uk puis vérifie que chaque arête du graphe est bien adjacente à un de ces sommets.
Pour montrer que le problème VERTEX-COVER est NP-difficile, on va réduire polynomialement le problème 3-SAT à VERTEX-COVER. À chaque instance de 3-SAT, on associe une instance de VERTEX-COVER qui a une solution si et seulement si l'instance de 3-SAT en a une. Soit φ une instance de 3-SAT, c'est-à-dire une formule en forme conjonctive telle que chaque clause de φ contienne trois littéraux. On note k le nombre de clauses de φ et m le nombre de variables apparaissant dans φ.
À cette formule φ, on associe un graphe non orienté ayant 3k+2m sommets. Chaque sommet du graphe est en outre étiqueté par un littéral. À chaque variable xi correspondent deux sommets étiquetés par les littéraux xi et ¬xi. Ces deux sommets sont reliés par une arête. Cette partie du graphe est appelée le gadget de la variable xi. À chaque clause correspondent trois sommets, un étiqueté par chaque littéral de la clause. Ces trois sommets sont reliés entre eux par trois arêtes. On ajoute en outre une arête entre chacun des trois sommets d'une clause et le sommet de la variable qui étiqueté par le même littéral. Cette partie du graphe est appelée le gadget de la clause.
La construction est illustrée sur la formule φ = (x0 ∨ x1 ∨ x2) ∧ (¬x0 ∨ ¬x2 ∨ x3) ∧ (x1 ∨ x2 ∨ ¬x3). Les entiers k et m sont égaux à 3 et 4 et on obtient le graphe représenté à la figure ci-dessous.
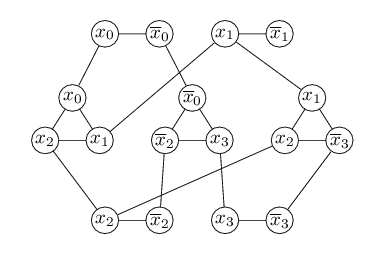
Fig. 2 : graphe associé à la formule φ
Nous allons voir que la formule φ est satisfiable si et seulement si le graphe G contient une couverture de taille 2k+m. Pour chaque variable xi, il faut qu'un des deux sommets associés soit dans la couverture pour couvrir l'arête entre ces deux sommets. De même pour chaque clause, il faut que deux des trois sommets associés soient dans la couverture pour couvrir les trois arêtes entre ces sommets. Ceci montre qu'une couverture du graphe doit contenir au moins 2k+m sommets.
Supposons d'abord que la formule φ est satisfiable. Il existe donc une affectation des variables telle que φ vaille 1. Ceci signifie qu'au moins un littéral par clause vaut la valeur 1. Pour chaque variable xi, on met dans la couverture le sommet xi ou le sommet ¬xi suivant que xi vaille 1 ou 0 dans l'affectation. Pour chaque clause, on met dans la couverture deux sommets du gadget correspondant en prenant au moins les littéraux qui ont la valeur 0 et d'autres pour compléter. Ces choix construisent une couverture. Toutes les arêtes à l'intérieur des gadgets sont couvertes. Chaque arête entre les gadgets des variables et des clauses, relie une variable au littéral correspondant. Si la variable vaut 1, le sommet dans le gadget de la variable a été choisi et si la variable vaut 0,le sommet dans le gadget de la clause a été choisi. Dans les deux cas, l'arête est couverte.
Supposons maintenant que G possède une couverture de taille 2k+m. Il est clair que cette couverture a exactement un sommet dans chaque gadget associé à une variable et deux sommets dans chaque gadget associé à une clause. Il est facile de vérifier que le choix des sommets dans les gadgets des variables définit une affectation qui donne la valeur 1 à la formule φ.
Un chemin hamiltonien dans un graphe G est un chemin qui passe une fois et une seule par chaque sommet de G. Le problème du chemin hamiltonien (appelé HAM-PATH) est de savoir si un graphe G donné contient un chemin hamiltonien de s à t pour deux sommets s et t également donnés. Ce problème peut être posé pour un graphe orienté ou pour un graphe non orienté mais ces deux problèmes se ramènent aisément de l'un à l'autre.
Proposition. Le problème HAM-PATH est NP-complet.
Le problème HAM-PATH est dans NP. Un algorithme pour résoudre ce problème commence par choisir de façon non déterministe une suite de u1, …, un de sommets puis vérifie ensuite qu'il s'agit d'un chemin hamiltonien de s à t.
Pour montrer que le problème HAM-PATH est NP-difficile, on va réduire polynomialement le problème 3-SAT à HAM-PATH. À chaque instance de 3-SAT, on associe une instance de HAM-PATH qui a une solution si et seulement si l'instance de 3-SAT en a une. Soit φ une instance de 3-SAT, c'est-à-dire une formule en forme conjonctive telle que chaque clause de φ contienne trois littéraux. On note k le nombre de clauses de φ et m le nombre de variables apparaissant dans φ. Si une variable apparaît positivement et négativement dans la même clause, cette clause est toujours satisfaite. On suppose dans la suite que chaque variable apparaît au plus une fois dans chaque clause.
À cette formule φ, on associe un graphe orienté ayant 2km + 2m + k sommets. À chaque clause est associé un seul sommet. À chaque variable est associé une partie du graphe appelé gadget. Pour chaque variable, ce graphe possède 2k+2 sommets et est identique à celui représenté sur la figure ci-dessous.
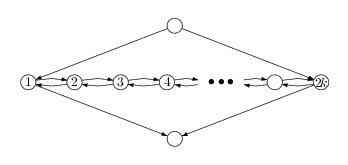
Fig. 3 : gadget associé à une variable
Le graphe global est obtenu en mettant bout à bout les gadgets pour obtenir une sorte de chapelet et en ajoutant les sommets des clauses. Le gadget d'une variable est relié au sommet de chaque clause où elle apparaît. Si la variable apparaît positivement dans la j-ième clause, il y a une arête du sommet 2j-1 du gadget vers le sommet de la clause et une arête du sommet de la clause vers le sommet 2j du gadget. Si la variable apparaît négativement dans la j-ième clause, il y a une arête du sommet 2j du gadget vers le sommet de la clause et une arête du sommet de la clause vers le sommet 2j-1 du gadget.
Le sommet s est le premier sommet du gadget de la première variable et le sommet t est le dernier sommet du gadget de la dernière variable. On vérifie qu'il y a un chemin hamiltonien dans la graphe construit si et seulement si la formule φ est satisfiable.
La construction est illustrée sur la formule φ = (x0 ∨ x1 ∨ x2) ∧ (¬x0 ∨ ¬x2 ∨ x3) ∧ (x1 ∨ x2 ∨ ¬x3). Les entiers k et m sont égaux à 3 et 4 et on obtient le graphe représenté à la figure ci-dessous.
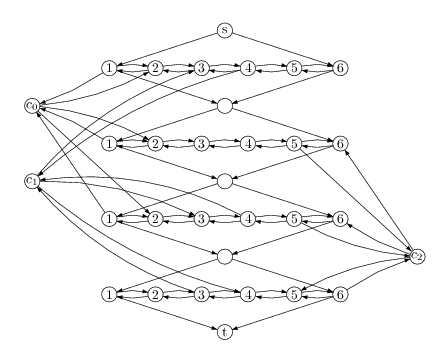
Fig. 4 : graphe associé à la formule φ
Le problème de la somme (appelé SUBSET-SUM) est le suivant. Une suite d'entiers x1, …, xk ainsi qu'un entier s sont donnés. Le problème est de savoir s'il est possible d'extraire une sous-suite de la suite donnée de manière à obtenir une suite dont la somme est égale à s. La solution est donc une suite croissante d'entiers 1 ⩽ i1 < i2 < ⋯ < in ⩽ k telle que
xi1 + xi2 + ⋯ + xin = s
Proposition. Le problème SUBSET-SUM est NP-complet.
Le problème SUBSET-SUM est dans NP. Un algorithme pour résoudre ce problème commence par choisir de façon non déterministe les indices i1, i2, …, in puis vérifie que la somme xi1 + … + xin a pour valeur s.
Pour montrer que le problème SUBSET-SUM est NP-difficile, on va réduire polynomialement le problème 3-SAT à SUBSET-SUM. À chaque instance de 3-SAT, on associe une instance de SUBSET-SUM qui a une solution si et seulement si l'instance de 3-SAT en a une. Soit φ une instance de 3-SAT, c'est-à-dire une formule en forme conjonctive telle que chaque clause de φ contienne trois littéraux. On note k le nombre de clauses de φ et m le nombre de variables apparaissant dans φ. Soient c0, …, ck-1 les k clauses de φ et soient x0, …, xm-1 les m variables de φ. Pour une variable xi de variable on note p(i) l'ensemble des numéros des clauses où xi apparaît positivement et n(i) l'ensemble des numéros des clauses où xi apparaît négativement.
A cette formule φ, on associe un ensemble de 2(m+k) entiers qui vont s'écrire avec m+k chiffres en base 10. À chaque variable xi correspond deux entiers ni et pi définis de la façon suivante.
ni = 10k+i + ∑j ∈ n(i)
10j
pi = 10k+i + ∑j ∈ p(i)
10j
Les entiers ni et pi s'écrivent en base 10, avec m+k chiffres égaux à 0 ou 1. Pour ni, le chiffre à la position k+i et les chiffres aux positions de n(i) sont des 1 et tous les autres chiffres sont des 0. Pour pi, le chiffre à la position k+i et les chiffres aux positions de p(i) sont des 1 et tous les autres chiffres sont des 0.
A chaque clause cj, on associe deux entiers qj et q'j qui sont tous les deux égaux à 10j. Les entiers qj et q'j s'écrivent en base 10, avec k chiffres égaux à 0 ou 1. Le chiffre à la position j est un 1 et tous les autres sont des 0.
On définit le nombre s par la formule suivante.
s = ∑0 ⩽ i < m 10k+i + 3 ∑0 ⩽ j < k 10j
L'entier s s'écrit en base 10 avec des chiffres 1 et 3. Son écriture en base 10 a la forme 1…13…3 où le premier bloc comporte m chiffres 1 et le second bloc comporte k chiffres 3.
Nous allons illustrer cette construction sur la formule φ = (x0 ∨ x1 ∨ x2) ∧ (¬x0 ∨ ¬x2 ∨ x3) ∧ (x1 ∨ x2 ∨ ¬x3). Les entiers k et m sont égaux à 3 et 4. Les entiers n0, p0, n1, p1, n2, p2, n3, p4, q0, q1, q2 et s sont donnés ci-dessous.
| n | x3 | x2 | x1 | x0 | c2 | c1 | c0 | Valeur | n0 = | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1001 |
|---|---|---|---|---|---|---|---|---|
| p0 = | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1010 |
| n1 = | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 10101 |
| p1 = | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 10000 |
| n2 = | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 100101 |
| p2 = | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 100010 |
| n3 = | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1000010 |
| p3 = | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1000001 |
| q0, q'0 = | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| q1, q'1 = | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 10 |
| q2, q'2 = | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 100 |
| s = | 1 | 1 | 1 | 1 | 3 | 3 | 3 | 1111333 |
La preuve que l'instance du problème SUBSET-SUM a une solution si et seulement si la formule φ est satisfiable découle des remarques suivantes. La première remarque est que pour chaque colonne, il y a au plus cinq entiers qui ont un chiffre 1 dans cette colonne. Ceci signifie que quelque soit le choix des entiers, leur somme se fait sans retenue. La somme est donc calculée colonne par colonne.
Comme le chiffre de s est 1 dans chaque colonne associée à la variable xi, il est nécessaire d'utiliser exactement un des deux entiers ni et pi. Ce-sont en effet les seuls qui ont un chiffre non nul dans cette colonne et il n'est pas possible de prendre les deux. Le fait de prendre de choisir ni ou pi correspond à affecter la valeur 0 ou 1 à la variable xi. Chaque entier ni ou pi ajoute 1 dans chaque colonne associée à une clause égale à 1 pour le choix de la valeur de la variable xi. Comme le chiffre de s est 3 dans chaque colonne associée à clause cj, il faut exactement trois entiers qui apportent une contribution dans cette colonne. Deux contributions peuvent être apportées par qj et q'j mais une contribution au moins doit être apportée par un entier ni et pi. Ceci garantit que toutes les causes sont vraies. Si plusieurs variables rendent vraie la même clause, on adapte la somme dans cette colonne en retirant un ou deux des entiers qj et q'j.