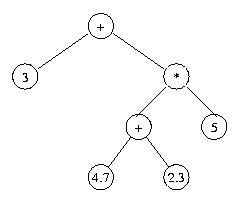
FIG 1. L'arbre de l'expression 3 + (4.7 + 2.3) * 5
En plus des points et des rectangles vus au séances précédentes, on s'intéresse maintenant aux disques. On considère qu'un disque est déterminé par son centre et son rayon.
Définir une classe Disque avec des constructeurs appropriés ainsi que des méthodes translate, surface et contains.
Aux séances précédentes avait été définie une classe Dessin qui permettait de regrouper des rectangles.
Quelle est la bonne méthode pour avoir des dessins capables de regrouper à la fois des rectangles et des disques. On pourra utiliser une interface Figure.
La classe Dessin possède des méthodes translate, surface et contains. Peut-elle implémenter l'interface Figure ? Quel est l'intérêt de faire cela ?
On considère maintenant des expressions arithmétiques formées à partir de constantes réelles (nombres flottants) et utilisant les quatre opérations arithmétiques usuelles (addition, soustraction, multiplication et division). Un telle expression est par exemple 3 + (4.7 + 2.3) * 5 .
Ces expressions arithmétiques sont représentés par des arbres binaires. Les nœuds internes de l'arbre contiennent les opérateurs alors que Les feuilles de l'arbre contiennent les constantes. Les fils gauche et droit d'un nœud interne représentent les deux sous-expressions gauche et droite. L'expression 3 + (4.7 + 2.3) * 5 par l'arbre de la figure ci-dessous.

FIG 1. L'arbre de l'expression 3 + (4.7 + 2.3) * 5
Définir une interface ArithExpr qui déclare les fonctionnalités d'une expression arithmétique. La seule fonctionnalité requise est de pouvoir être évaluée. Déclarer en conséquence une méthode eval du bon type.
Pour représenter l'expression, on va créer des objets pour chacun des nœuds. Ces objets vont bien sûr être des instances de classes différentes suivant qu'il s'agisse de nœuds internes ou de feuilles.
Définir une classe Constant pour représenter les constantes des expressions.
Définir quatre classes Addition, Soustraction, Multiplication et Division pour les opérations arithmétique. On remarque que ces quatre classes partagent beaucoup de propriétés. Comment faut-il faire pour partager le code ?
Redéfinir la méthode toString afin d'afficher les expressions en notation infixe. Écrire des méthodes prefix et suffix permettant d'afficher les expressions en notation préfixe et suffixe.
Que faut-il ajouter pour que les expressions arithmétiques puissent contenir des variables comme dans l'expression 3 * x + 7 ? Comment définir la méthode eval pour une variable ?
La lecture d'une expression arithmétique se fait par l'intermédiaire d'un parseur. Un parseur est un objet capable de créer une expression arithmétique à partir d'une chaîne de caractères.
Définir une classe abstraite ArithExprParser ayant deux méthodes parse. La première méthode prend en paramètre une chaîne de caractères alors que la seconde prend un Reader.
Écrire une classe PrefixParser permettant de lire une expression arithmétique en notation préfixe.
Écrire une classe InfixParser permettant de lire une expression arithmétique en notation infixe.