ERC Starting Grant
CombiTop
–
New Interactions of Combinatorics
Through Topological Expansions
The 5-year project CombiTop, funded by the ERC (Starting Grant 2016) started in 2017. It is centered around, but not limited to, the combinatorics of maps on surfaces, and more precisely the combinatorics arising in topological expansions (roughly speaking, 2D counting problems where the dependence on the genus invariant plays a central role).
The main goal is to study the interactions between:
- the bijective approach to maps;
- random maps and Brownian maps;
- the "combinatorics of fermions", tau functions, symmetric group algebra and algebraic combinatorics;
- the combinatorics of the topological recursion.
Each of these topics features some remarkable integrability properties as well as some beautiful combinatorial constructions, and the main goal of the project is to seek for a greater unification of these theories, including their combinatorial aspects.
Project members or ex-members
- Guillaume Chapuy (Principal Investigator)
- Séverin Charbonnier (Postdoc, 2021-2022)
- Harriet Walsh (PhD student)
- Elba Garcia-Failde (Postdoc, 2020-2021)
- Baptiste Louf (PhD student, 2017-2020)
- Theodosios Douvropoulos (Postdoc, 2017-2020)
- Luca Lionni (Postdoc, 2019)
- Cyril Marzouk (Postdoc, 2018-2019)
News: Journée de l'ERC CombiTop le 15 février 2019 à l'IRIF: quatre orateur·trice·s aborderont les cartes dans leurs aspects combinatoires, probabilistes, et physiques. Inscription obligatoire avant le 1er février, voir ici.
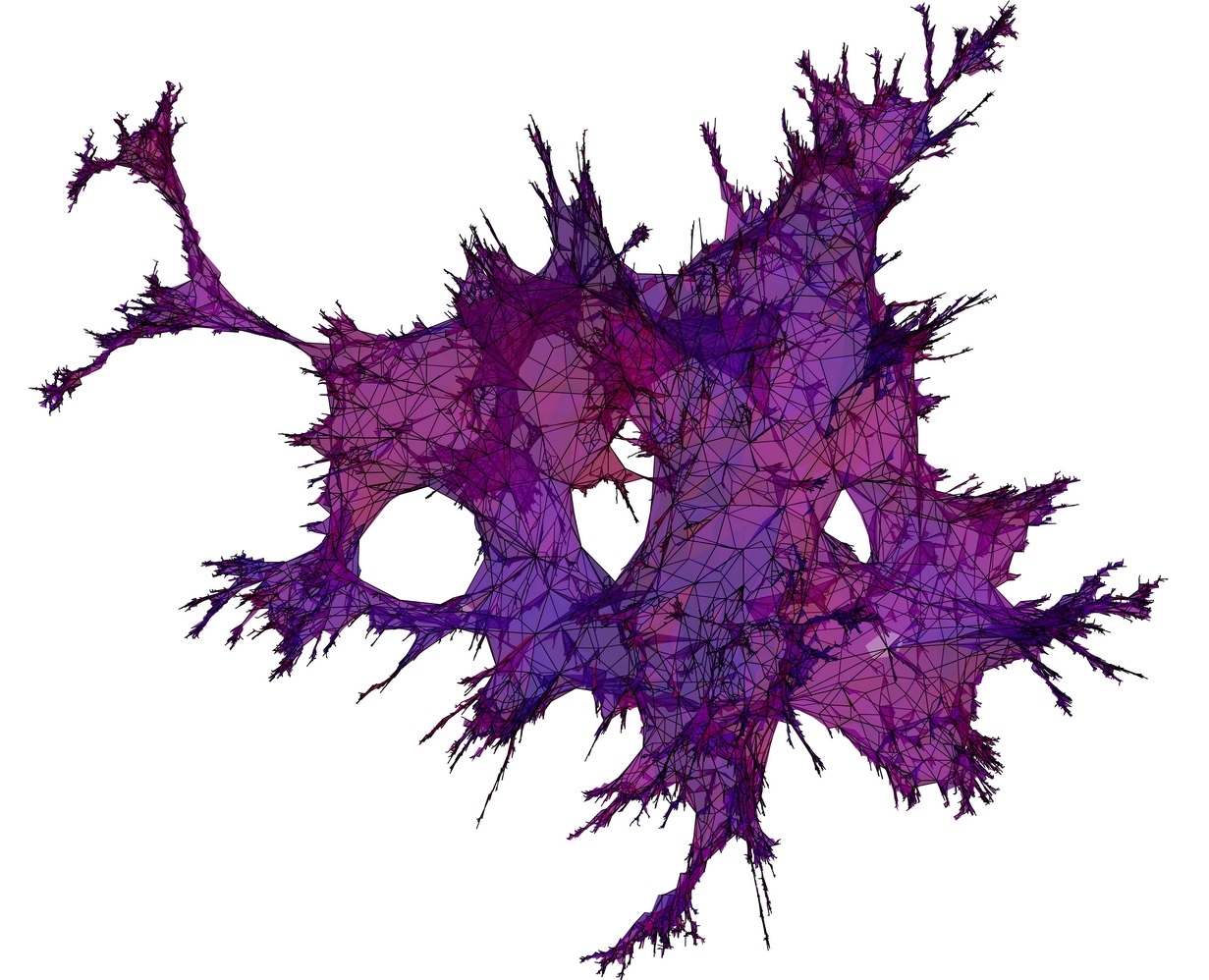
Credit for the (purple) genus-3 Brownian map image at the top of this page: Jérémie Bettinelli.
The project CombiTop receives funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. ERC-2016-STG 716083).