The case of triangulations: derivation of the ODE (Prop 4.8, Thm 4.10, Thm 4.11)  

>

# Proposition 4.8 (proved in the paper) # computes recursively theta_3 F_lambda as a differential polynomial in Xi(t). # here L = [i,2^n2,1^n1] and i<=8, otherwise it will probably crash or at least loop forever # Computes \theta_3 F_\lambda as a differential operator in \Xi(t,u,z) FTth:=proc(L) option remember; local i,j,Lcut, Lcutj, res,n; if nops(L)=0 then  return Xi(t); else  i:=max(L)-3;  Lcut:=subsop(ListTools:-Search(i+3, L)=NULL, L);     # if i=0 we chose to remove a part equal to i+3=3 using Eq (36)  if i=0 then    return t/3/z*diff(FTth(Lcut),t) - add(Lcut[ii],ii=1..nops(Lcut))/3/z*FTth(Lcut):  fi:  # if i=-2 then all parts are equal to 1 and we use (37)  if i=-2 then    res:=t^5*z*diff(FTth(Lcut),t):    if nops(Lcut)=0 then res:=res+t^4*z*(u^2+u)/2; fi:    if nops(Lcut)=1 then res:=res+t^2*u/2; fi:    return res;  fi:  # in other cases we use (35)  for j from 1 to 2 do  n[j]:=ListTools:-Occurrences(j,Lcut); od;  res:=    -2*t^2*add(add(add(             a*(i-a)*binomial(n[1],l1)*binomial(n[2],l2)             *FTth([a,seq(2,ii=1..l2),seq(1,ii=1..l1)])             *FTth([i-a,seq(2,ii=1..n[2]-l2),seq(1,ii=1..n[1]-l1)])          ,l1=0..n[1]),l2=0..n[2]),a=1..i-1)   -2*t^2*add(a*(i-a)*FTth([a,i-a,op(Lcut)]),a=1..i-1)   +(i+2)*FTth([i+2,op(Lcut)]);   # this loop implements the sum over j=1..2 in the paper   for j from 1 to 2 do     if n[j]*(i+j)<>0 then     # Lcut with one occurrence of j removed      Lcutj:=subsop(ListTools:-Search(j, Lcut)=NULL, Lcut):      res:= res-t^2*n[j]*(i+j)*FTth([i+j,op(Lcutj)]):     fi;   od:   # terms with Kronecker deltas   if i<>-1 then    res:=res-(2*u+i+1)*i*FTth([i,op(Lcut)])*t^2   fi;   if n[2]=0 then    if i=-1 and n[1]=1 then res:=res-u/2*t^2;    elif i=0 and n[1]=0 then res:=res-(u+1)*u/2*t^2;    fi:   fi:  return collect(simplify(res/z/t^2/(i+3)),diff); fi; end:

 

>	# Example of computation expand(FTth([4,1]));

 

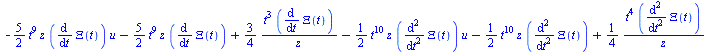(3.5.1)

 

>

# ODE of Theorem 4.10 -- automated computation via Prop 4.8 KP1:= - 4*FTth([3,1]) + 4*FTth([2,2])        + 4/3*(6*FTth([1,1])^2+FTth([1,1,1,1])): KP2:= - 4*FTth([4,1]) + 4*FTth([3,2])        + 8/3*(6*FTth([2,1])*FTth([1,1])+FTth([2,1,1,1])): KP3:= - 6*FTth([5,1]) + 4*FTth([4,2]) + 2*FTth([3,3])        + 8/3*(6*FTth([3,1])*FTth([1,1])+FTth([3,1,1,1]))        + 4*(4*FTth([2,1])^2+2*FTth([2,2])*FTth([1,1])+FTth([2,2,1,1]))       + 4/45*(60*FTth([1,1])^3+30*FTth([1,1,1,1])*FTth([1,1])                +FTth([1,1,1,1,1,1])): t^10*z^2*diff(KP1,t)^2 -KP2^2 + KP1* ( KP3-1/2/t^2/z*KP2  -t^10*z^2*diff(KP1,t,t)  -5*t^9*z^2*diff(KP1,t)  -2*t^10*z^2*diff(Xi(t),t,t)*KP1  -10*t^9*z^2*diff(Xi(t),t)*KP1  -4*t^8*z^2*(u^2+u)*KP1  -t^2*u*KP1 ): # because z is redundant with t everywhere # and in view of forthcoming calculations, we just set z=1 in the ODE subs(z=1,%): bigODEtriangulations:=factor(%/t^5): # this ODE has many terms ! nops(bigODEtriangulations);

 

(3.5.2)

 

>

 

>

# Check of Thm 4.11 # To check the precise form of Thm 4.9 we need to examine the top-degree part of the ODE # This is analogue to the proof of Thm 1.2 and 4.6 above # The exponent of t is 6n and the exponent of u is k=n+2-2g # Euler's formula gives 12g = 12 + (6n) - 6k. ODEscaled:= subs(u=u*beta^6,z=1,t=t/alpha/beta,subs(subs(seq(((D@@i)(Xi))(t)=Xi[i]*alpha^i*beta^(12+i),i=1..20),convert(bigODEtriangulations,D)))): # We check that there is a term realizing the highest power in BOTH alpha and beta # This proves that we get a recurrence of the form # T[n,g] = (expression involving only terms with g'<=g, n'<=n) degree(ODEscaled,alpha),degree(ODEscaled,beta); factor(coeff(coeff(ODEscaled,alpha,1),beta,25)); # The more precise form given in thm 4.11 (explicit expression of all terms involving the highest total size) # is equivalent to knowing the highest alpha power: collect(coeff(ODEscaled,alpha,1),beta);

 

 

 

	(3.5.3)