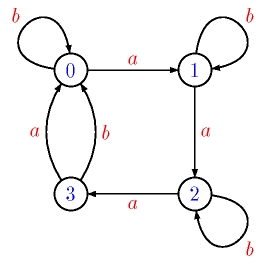
Figure 1. A synchronizing automaton with 4 states.
|
|
Let A = (Q, A, .) be a deterministic automaton with n states (the initial state and the final states do not play any role in this conjecture). A word w is said to be synchronizing in A if there exists a state p in Q such that, for every q in Q, q.w = p. For instance, in the automaton represented below, the word ba3ba3b is synchronizing, since 0.ba3ba3b = 1.ba3ba3b = 2.ba3ba3b = 3.ba3ba3b = 0. An automaton is synchronizing if it admits a synchronizing word.

Cerný's conjecture states that if an n-state automaton is synchronizing, then it admits a synchronizing word of length ≤ (n-1)2. In our example, the word ba3ba3b has length 9 = (4-1)2.
In 1978, I proposed the following generalisation of Cerný's conjecture. Let A be an n-state automaton. Each word w defines a map from Q to Q. The rank of w in A is the size of its image (or codomain). Its deficiency in A is the integer n-k. The deficiency of A is the minimum of the deficiency of a word in A. For instance, if Ais the automaton represented in Figure 1, the word w = ba3b has rank 2, since 0.w = 0, 1.w = 0, 2.w = 1 and 3.w = 0. The deficiency of w is 2 = 4 - 2. The deficiency of A is 1. The computation of all the images of our example is done in Figure 2.
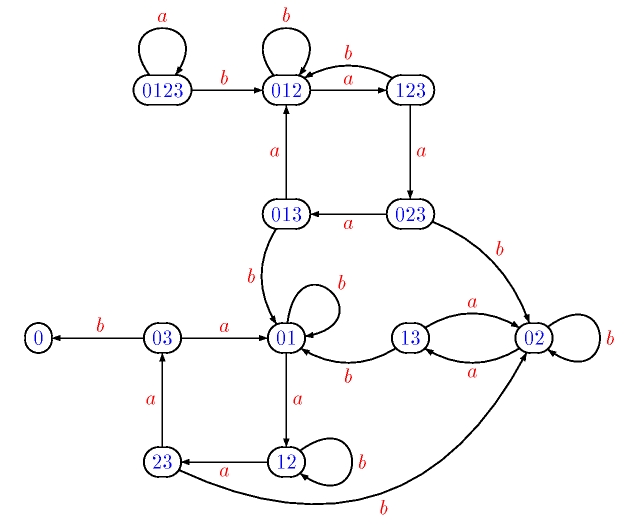
In our example, n = 4 and, for k = 0, the empty word (of length 0) has rank 4 = n - 0, the word b (of length 1) has rank 3 = (n-1), the word ba2b (of length 4 = (n-2)2) has rank 2 = (n-2) and the word ba3ba3b (of length 9 = (4-1)2) has rank 1 = (n-3). The conjecture can be stated as follows:Deficiency conjecture. If an automaton admits a word of deficiency ≥ k, then there exists such a word of length ≤ k2.Intuitively, it means for instance that a word of length ≤ 9 should suffice to reach rank 7 in a 10-state automaton and that the same length 9 should suffice to reach rank 9997 in a 10000-state automaton. Cerný's conjecture corresponds to the case k = n-1.
The conjecture was proved to be true for k = 0, 1, 2, 3 but a counterexample, shown in Figure 3, was found by Jarkko Kari for k = 4.
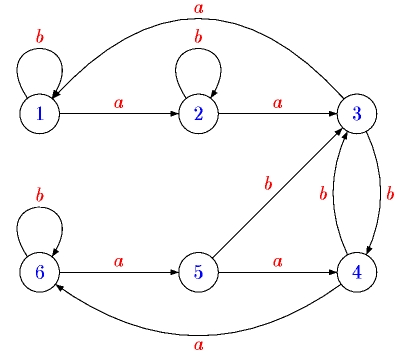
In this automaton, the shortest words of rank 2 are baabababaabbabaab and baababaabaababaab. Both have length 17, contradicting the upper bound (6-2)2 = 16.
In view of this counterexample, Volkov suggested to restrict the deficiency conjecture to automata of deficiency k.Volkov's deficiency conjecture. In an automaton of deficiency k there exists such a word of deficiency k and of length ≤ k2.No counterexample to this improved version of the deficiency conjecture has been found so far.
Cerný's conjecture was first stated in 1964. Various bounds have been obtained
2n - n - 1 (1964, Cerný )
1
2 n3 -
3
2 n2 + n + 1 (1966, Starke, 1969, Starke)
1
2 n3 - n2 +
n
2 (1970, Kohavi)
1
3 n3 - n2 -
1
3 n + 6 (1970, Paterson, personal communication to D.J. Kfoury)
1
3 n3 -
3
2 n2 +
25
6 n - 4 (1971, Cerný, Pirick· et Rosenauerova)
7
27 n3 -
17
18 n2 +
17
6 n - 3 for n multiple of 3 (1977, Pin)
1
6 n3
-
1
6 n - 1 (1983, Pin)
The best estimate on the deficiency conjecture known so far is due to Pin, 1983.
A word of deficiency ≥ k (in an automaton A) is also called k-deficient. An automaton is k-deficient if admits a k-deficient word. A word w in A* is universally k-deficient if its k-deficient in each k-deficient automaton A on the alphabet A.
Sauer and Stone proved in 1991 that universally n-deficient words exist for every n and every alphabet A. An open problem is to find, for each n and k, the length of a shortest universally n-deficient word on a k-letter alphabet.
For instance, it is shown in [Sauer and Stone, Corollary 3.4] that the word aba2b2ab is universally 2-deficient, and it can be checked that except this word and its mirror image, no word of length 8 over {a, b} is universally 2-deficient.