A Schreier formula for the free
monoid
(Conjecture proposed by Dominique Perrin)
|
Let A be a finite alphabet and let X be a finite subset of
A*. Let f : A* --> M be the
syntactic morphism of X* and let G be a maximal
group in M such that f-1(G) is not a cyclic
submonoid of A* (i.e., not of the form
u* for some word u). Such a group admits a
faithful representation as a permutation group. Let r be the rank
(that is, the minimal number of generators) of G, let d be
its degree and let c = Card(X).
Conjecture: d(r-1) ≤ c-1
Reminder. The Schreier formula states that if F is a free
group of rank r and H is a finitely generated subgroup of
rank c and degree d, then c-1 = d(r-1).
Example. Let X = {aaa, ba, abaa, aab}. The minimal automaton
of X* is represented in Figure 1.
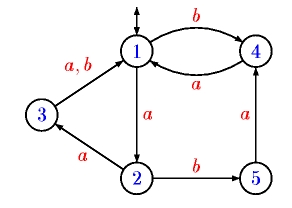
Figure 1. The minimal automaton of X*.
Then the words aa and aabaa generate a subgroup G of
M represented as a permutation group on {1, 2, 3}.
|
|
1
|
2
|
3
|
|
aa
|
3
|
1
|
2
|
|
aabaa
|
3
|
2
|
1
|
This group is actually the symmetric group S3. Here we
have c = 4, d = 3 and r = 2. Thus 3(2-1) = d(r-1)
≤ c-1 = 3.
The conjecture has been recently proved for r = 2 if X is a prefix code.
See [3] for more details.
References.
- Dominique Perrin, Sur les groupes dans certains les monoïdes
finis, Non commutative structures in Algebra and Geometric
Combinatorics, Quaderni de la Ricerca scientifica 109, CNR,
Roma (1981), 27--36.
- Dominique Perrin and Jean-François Perrot, A propos des
groupes dans certains monoïdes syntactiques, Lecture Notes in
Mathematics 855, Springer, Berlin (1980), 82--91.
- Dominique Perrin and Giuseppina Rindone, On
syntactic groups, Bull. Belg. Math. Soc. Simon Stevin 10 (2003),
suppl., 749-759.
- Dominique Perrin and Marcel Paul Schützenberger, Codes et
sous-monoïdes possédant des mots neutres. Rapport IRIA 214
(1977)
- Giuseppina Rindone, Sur les groupes syntaxiques d'un langage,
RAIRO Informatique Théorique 19, (1985), 57-70.
- Marcel Paul Schützenberger, The critical factorization
theorem, Chap. 8 in M. Lothaire, Combinatorics on Words, Cambridge
University Press, 1982.
Last modified 03/29/2008

