Gallery
One main ambition of my work is
to understand how formal proofs
should be written down.
This simple question is related to a myriad
of fascinating problems at the
interface of proof theory,
games semantics, n-dimensional algebra,
and mathematical physics.
For instance, I like to think that « game semantics »
is not just another « semantics » for proofs.
I prefer to see it as a « syntax ».
Of course, this « game syntax »
is a new kind of syntax, which does not look
like the previous ones -- especially if one thinks
of Frege's ideography, Gentzen's sequent calculus,
or even Girard's proof-nets.
This new brand of diagrammatic syntax
is at the same time
a « combinatorics »
of proofs, akin to the familiar structure
of topological knots in mathematics.
The wonderful thing is that we have
at our disposal, today, a large amount
of tools coming from algebra and
mathematical physics, to analyze that kind
of diagrammatic situation.
I am confident that this point of view
will deeply transform Proof Theory
as well as Programming Language Semantics.
There are also good reasons to believe
that this fresh air coming from algebra
and mathematical physics will not be confined to Proof Theory:
it should also benefit the other fields
of mathematical logic.
Here, I will limit myself to showing you
a few diagrams which I have drawn in my work.
Some of them describe proofs,
others describe structures of connectives
or modalities.
I have decided to show them here
mainly to entertain my non-mathematician friends.
However, I will briefly indicate to the specialist
reader what kind of mathematical structures
are depicted below.
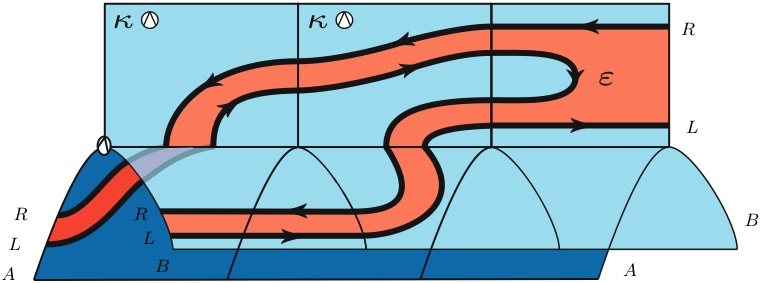
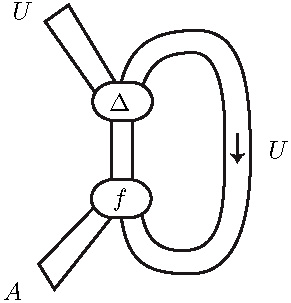
A proof in string diagrams
This is the proof that the conjunction of
the double negations of two formulas
A and B implies the double negation
of the conjunction of the two formulas.
Note that the trajectories of the negations
R and L coincide with the strategy associated
to the proof in « game semantics ».
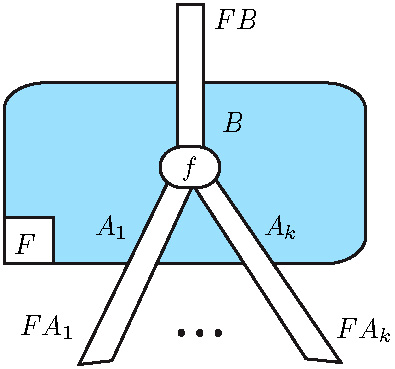
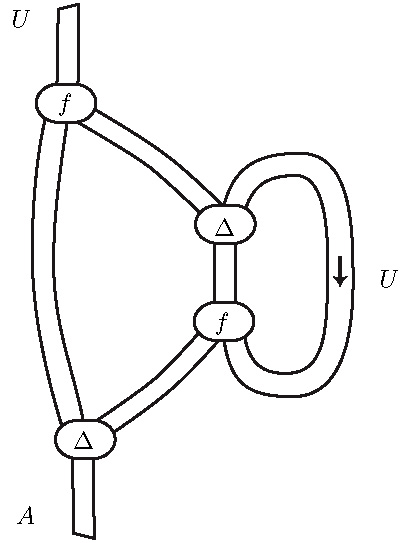
Modalities as boxes
I like to draw modalities as boxes, surrounding proofs:
intuitively, the modality encapsulates the proof, and
indicates a modal attitude to the external world.
Interestingly, these modal boxes have a clear
algebraic meaning: they model various kinds
of (monoidal) functors between (monoidal) categories.
I use this diagrammatic language to describe how
a proof duplicates another proof in linear logic.
This leads to nice diagrams, as this one above,
describing a contraction node interacting with
the principal door of an exponential box in linear logic.
The methodology extends quite nicely to broader
territories -- leading to natural extensions of
flowchart diagrams in programming language design.
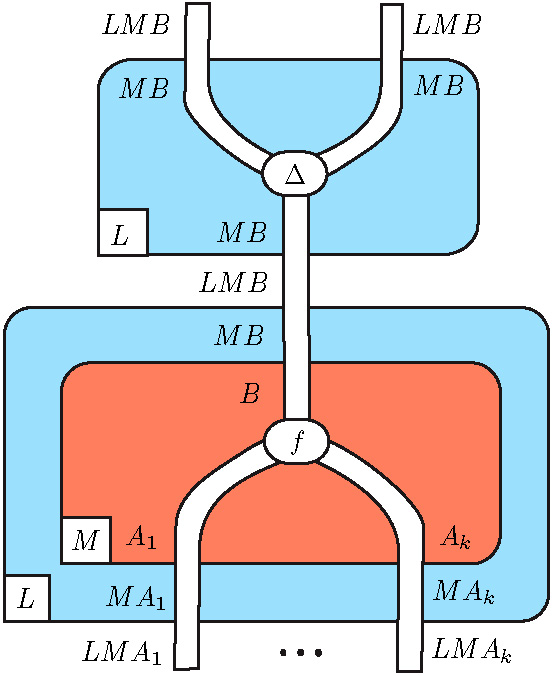
The structure of recursion
Martin Hyland and Masahito Hasegawa have
shown around 1996 that this construction
defines a (parametric) fixpoint operator
in any cartesian category with a trace operator --
typically, the category of Scott domains
and continuous functions.
This amounts to showing that the diagram above
is equal to the diagram below.
The diagram shows that every adjunction
does not simply define a monad, but in
fact what I like to call a «parametric monad ».
This structure captures precisely
the property of a logical implication
defined by negative translation --
as in the case of language defined by continuations.
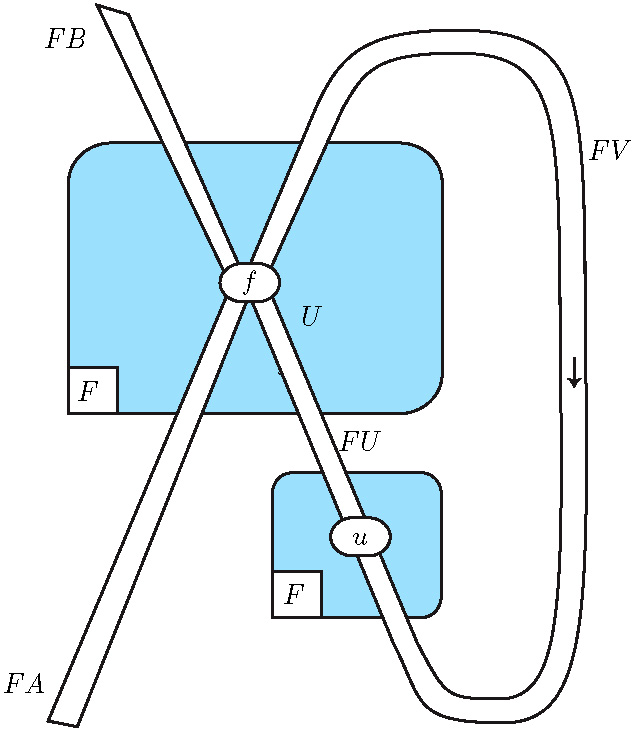
Associativity of the parametric monad
is established thanks
to a series of diagrams, involving this one:
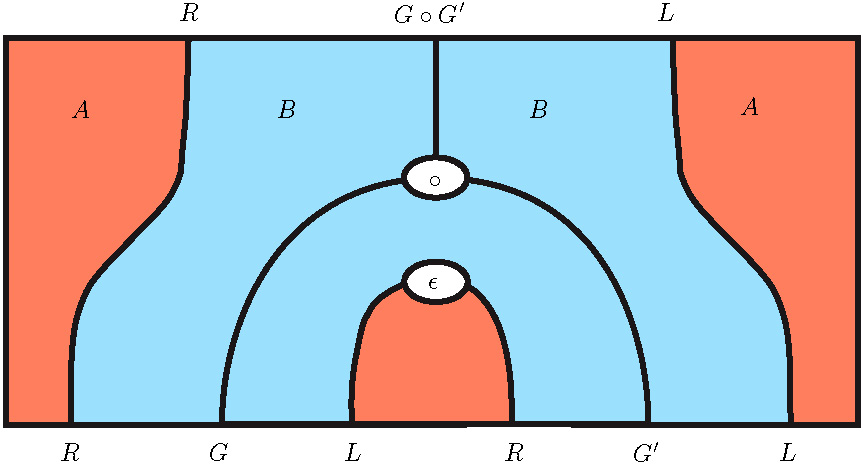
Monoidal fibrations in string diagrams
I have been thinking for a long time at the question of defining
a properly fibered version of linear logic and other monoidal proof systems
--- and more specifically tensor logic which underlies traditional game semantics.
The most natural way to proceed is to start from the usual notion of fibration,
and to observe that its algebraic structure may be depicted
in the 2-dimensional language of string diagrams.
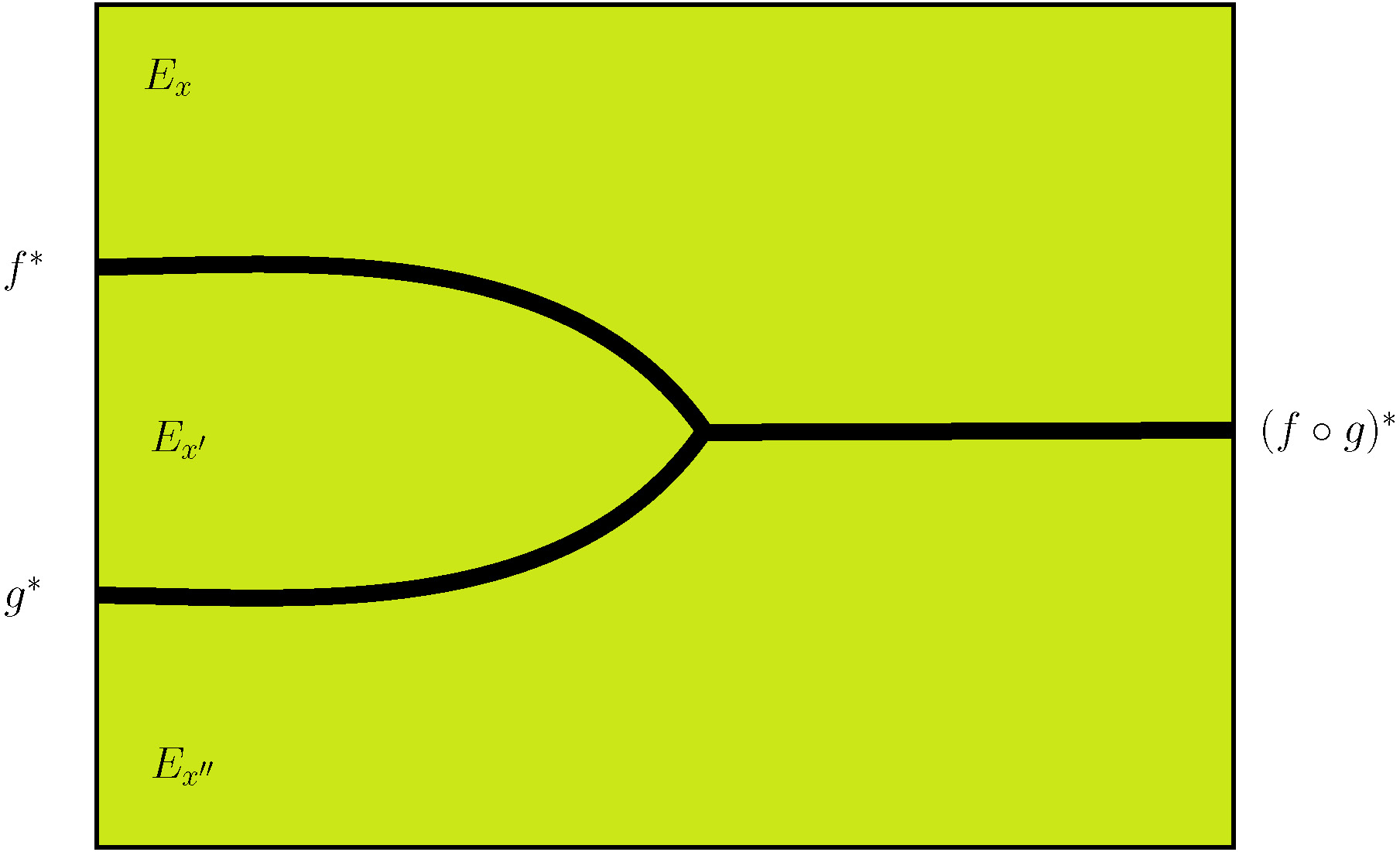
For instance, the diagram above describes the natural transformation
which enables to compose together two fiber functors.
In order to define the relevant version of monoidal fibration, it is important
to remember the lessons of proof systems like separation logic, and to resist
the (extremely bad) temptation to ask that every fiber is a monoidal category.
Indeed, the idea behind such a fibration is that a program uses the computational
resource offered by its fiber (typically a set of allocated memory cells).
Hence the tensor product of two programs should live inside the tensor product
of their two fibers, because this tensor product is precisely the resource
they need in order to achieve their task.
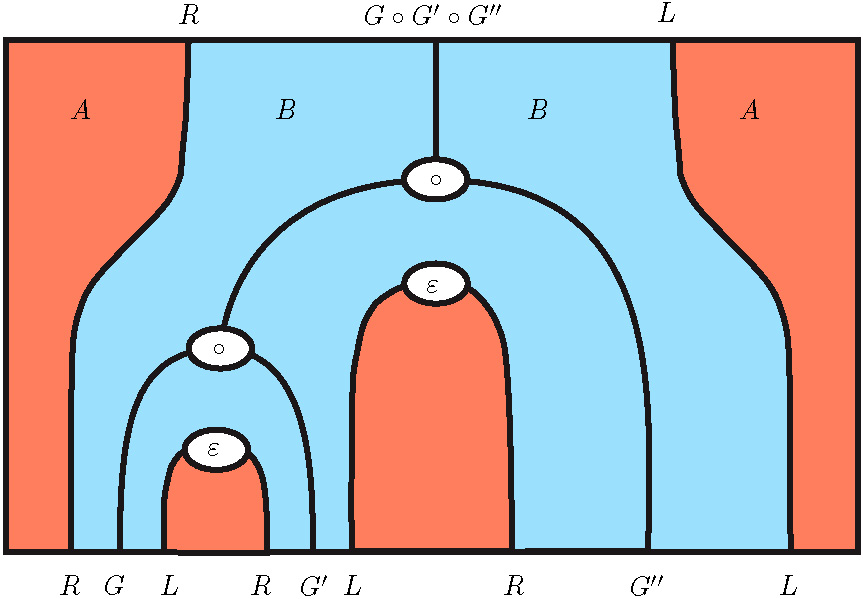
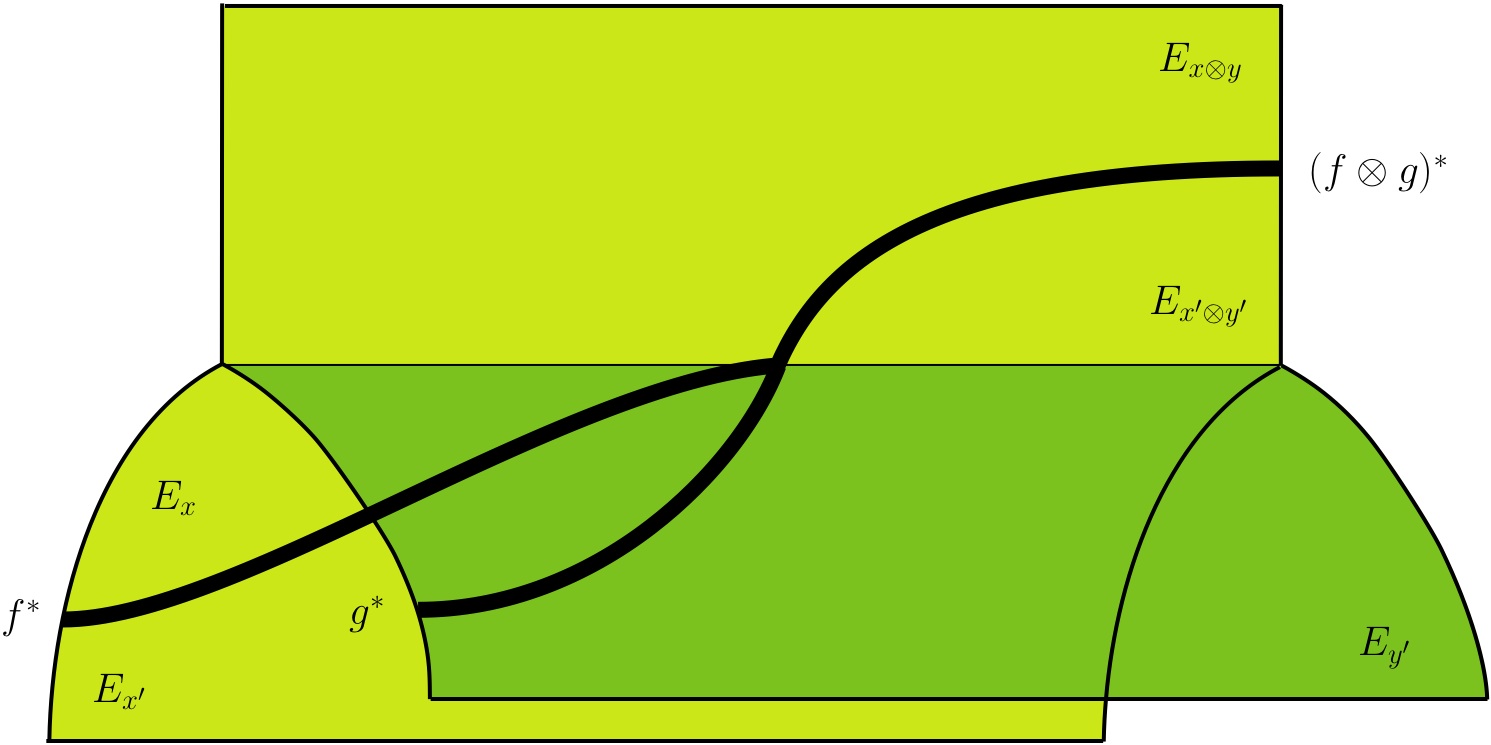
This line of thought leads to a very natural notion of monoidal fibration,
which requires to shift from the language of string diagrams to
the 3-dimensional language of surface diagrams.
For instance, the diagram above depicts the natural transformation
which enables to tensor together two independent fiber functors.
The notion of monoidal fibration is extremely natural... but strangely
enough I was not able to find the notion in the literature for a very
long time. It is only a few years ago that I discovered it with
great excitement (and relief!) in this
article
written by Mike Shulman --- where the notion of monoidal fibration
which I had in mind is formulated and studied from several angles.
Random walks on configuration spaces
This
applet
computes a random walk on the configuration space of an event structure
of 12 × 12 × 12 little cubes.
The random walk is carefully designed in order to converge
to the uniform distribution on the set of configuration spaces.
To that purpose, it follows the Glauber dynamics associated
to the distribution.
If you are sufficiently patient, you will see that the walk eventually
reaches a random sample where something like an artic circle separates
a liquid phase and a solid phase.
The very same story as above, but this time on a grid
of
25 × 25 × 25 little cubes,
or even
50 × 50 × 50 little cubes, depending on your taste and appetite.
Please have a look at the
tutorial
by Richard Kenyon if you want to know more about this fascinating topic.