Complexity Classes Beyond Elementary
Sylvain Schmitz
LSV, ENS Cachan & CNRS & INRIA
Queen Mary, December 11, 2013
Hitchhiker's Guide to Galactic Complexity
Don't panic
When I thought about it I found my original title a bit
too conservative...
The nice thing about this one is that I can write Don't
panic in large, friendly letters.
This is truly a talk aimed at my colleagues, who have to
deal with non-elementary problems, but feel uneasy with
the lack of appropriate complexity classes.
Complexity Classes
classify problems
master problems and reductions
hierarchies
$\CC{P}$
$\CC{NP}$
$\text{co-NP}$
SAT
3SAT
Tree Automata Emptiness
$\CC{P}$
$\Sigma_1^p$
$\Pi_1^p$
Complexity classes provide us with a meaningful
way of comparing and classifying problems.
Perhaps the best-known classes are $\CC{P}$ and $\CC{NP}$
and the million-dollar
question of their exact relationship.
Through the notions of
reductions
and completeness , complexity classes allow to
classify problems, as for instance in
the polynomial
hierarchy .
$\Pi_2^p$
$\Sigma_2^p$
$\Delta_2^p$
$\CC{PH}\\~~\vdots$
$\CC{PSpace}$
$\CC{EXP}$
$\CC{NEXP}$
$\text{co-NEXP}$
$\CC{ExpSpace}$
$\CC{R}$
$\CC{Elementary}$
$\vdots$
Lossy Channel System Reach. LCS
Safety MTL Sat. SMTL
Lossy Counter Machine Reach. LCM
MTL Finite Sat. FMTL
Post Embedding Problems PEP
WS1S Sat. WS1S
Equivalence of SF Exprs. SFEq
β-Equ. of Simply-Typed λ Terms SλEq
…
with $\CC{Elementary}$
as the union of the elementary classes; note that
it's not the limit of the exponential
hierarchy, and bears in some sense the same relationship to it
as $\CC{PH}$ to the polynomial hierarchy.
Now if you look at your classical book on complexity
theory, this is where it stops, anything decidable above
$\CC{Elementary}$ is
in $\CC{R}$ ,
(though sometimes people
mention $\text{Primitive-Recursive}$
as an intermediate step).
The issue then, is how to compare the known non-elementary
problems? Can you pinpoint them in this large no-man's
land?
Extended Grzegorczyk Hierarchy
[Löb & Wainer, 1970]
$\begin{aligned}
F_0(x)&\eqdef x+1
& \!\!\!\!\!\!F_1(x)&=2x+1\\
F_{\alpha+1}(x)&\eqdef F^{x+1}_\alpha(x)
&\!\!\!\!\!\!F_2(x)&=2^{x+1}(x+1)-1\\
F_\lambda(x)&\eqdef F_{\lambda(x)}(x)
&\!\!\!\!\!\!F_3(x)&\text{ non elementary}\\
&&\!\!\!\!\!\!F_\omega(x)&\text{ Ackermannian}\end{aligned}\\\begin{aligned}
\FGH{\alpha}&\eqdef\bigcup_{c<\omega}\CC{FDTime}\left(F_\alpha^c(n)\right)\\
\FGH{<\alpha}&\eqdef\bigcup_{\beta<\alpha}\FGH{\beta}
\end{aligned}$
In fact, it's not quite true that there is no
classification above $\CC{Elementary}$.
The fast-growing
hierarchy for instance has been used in recursion
theory, proof theory or rewriting theory to classify the
expressive power of various models. It allows to build an
ordinal-indexed hierarchy of classes of functions
that matches some well-known, robust landmarks above $\CC{Elementary}$.
$\CC{Multiply-Recursive}=\FGH{<\omega^\omega}^\ast$
$\CC{Primitive-Recursive}=\FGH{<\omega}^\ast$
$\CC{Elementary}=\FGH{2}^\ast$
Using the fast-growing
hierarchy, it has been possible in particular to
prove non-inclusion results: for
instance, LCS is not multiply-recursive,
and LCM is not primitive-recursive.
$\CC{HAck}\eqdef\FC{\omega^\omega}$
$\CC{Ack}\eqdef\FC{\omega}$
$\CC{Tower}\eqdef\FC{3}$
Our knowledge of these problems goes
however further:
using wqo
theory, we can prove upper bounds for these
problems. The missing ingredient is then to find appropriate
classes, such that the problems can be shown complete .
One can think of these classes as
limits : for instance, $\CC{Ack}$ is the class of non
primitive-recursive problems, but which are only barely
so.
Fast-Growing Complexity Classes
$\FC{\alpha}\eqdef\bigcup_{p\in\FGH{\lt\alpha}}\!\!\CC{DTime}\left(F_\alpha(p(n))\right)$
completeness for reductions in
$\FGH{\lt\alpha}$strict hierarchymany examples, using wqo length function
theorems for upper bounds
These classes are formally defined as those problems
computable by a Turing machine with resources (note that the
choice of time vs. space resources is rather irrelevant at
this complexity level!) bounded by the fast-growing function
$F_\alpha$ composed with some lower function
$p\in\FGH{\lt\alpha}$.
$\CC{Tower}=F_3$ is the class of problems of complexity
bounded by a tower of
exponentials, whose height is an elementary function of
the input,
$\CC{Ack}=F_\omega$ is the class of
Ackermannian problems and is closed under primitive-recursive
reductions.
These classes are deeply related to canonical
problems that use wqo theory in an essential way. See the
ESSLLI 2012
lecture notes with Ph. Schnoebelen to learn more on
this topic.
Example: $\CC{Tower}$
$\begin{aligned}\CC{Tower}\eqdef\FC{3}&=\bigcup_{p\in\FGH{2}}\CC{DTime}\left(F_3(p(n))\right)\\&=\bigcup_{p\in\CC{FElem}}\CC{Space}\left(\mathrm{tower}(p(n))\right)\\&\supsetneq\CC{Elem}=\bigcup_k k\CC{-ExpTime}\end{aligned}$
$\CC{Tower}$-complete problem: equivalence of
star free expressions (SFEq )
lower bound
acceptance of $\textrm{tower}(\log(n))$-space bounded Turing machines [Stockmeyer & Meyer, 1973]
upper bound automata-based construction
Example: $\CC{Ack}$
$\begin{aligned}\CC{Ack}\eqdef\FC{\omega}&=\bigcup_{p\in\FGH{<\omega}}\CC{DTime}\left(F_\omega(p(n))\right)\\&=\bigcup_{p\in\CC{FPR}}\CC{Space}\left(\mathrm{Ack}(p(n))\right)\\&\supsetneq\CC{PR}=\bigcup_k \FC{\,k}\end{aligned}$
$\CC{Ack}$-complete problem: reachability in lossy counter machines (LCM )
lower bound
halting of $F_\omega$-space bounded Minsky machines [Schnoebelen, 2010]
upper bound
length function theorem for Dickson's Lemma
LCM Reachability
lossy counter machines Minksy machines with a lossy semantics for steps over $Q\times\mathbb{N}^C$:$(q,\!\vec{v})\!\to_{\mathrm{lossy}}\!(q'\!,\!\vec{v}'\!)$ if $(q,\!\vec{v})\geq(q,\vec u)\!\to_{\mathrm{Minsky}}\!(q'\!,\!\vec{u}'\!)\geq(q'\!,\!\vec v')$
decidability of $\sigma\to^\ast_{\mathrm{lossy}}\tau$
LCM Reachability: Upper Bound
length function theorem
minimal witnesses are controlled : $\|\sigma_{i+1}\|_\infty\leq 1+\|\sigma_i\|_\infty$
maximal length of a bad controlled witness: bounded by $\ell=F_{\omega}(p(\max\{\|\tau\|_\infty,|Q|,|C|\}))$
for some polynom $p$
combinatorial algorithm
compute $\ell$
nondeterministically guess forward steps $\sigma=\sigma_0\to_{\mathrm{lossy}}\cdots\to_{\mathrm{lossy}}\sigma_n=\tau$
with $n\leq\ell$
LCM Reachability: Lower Bound
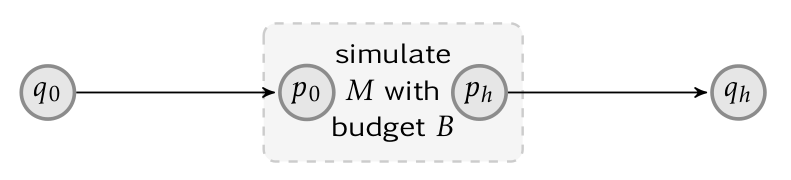
reduction from the halting problem of a $F_\omega(n)=F_{n+1}(n)$ bounded Minsky machine $M$
weakly compute $B\leq F_{n+1}(n)$weakly simulate $M$ with budget $B$; resulting budget $B'\leq B$weakly compute $n'\leq F_{n+1}^{-1}(B')$if $n'=n$, then no losses!
Computation snapshot for $F_{n+1}(n)$:
$F^{k_n}_n(F^{k_{n-1}}_{n-1}(\cdots
F^{k_0}_0(B)\cdots))$
Strictness
For $c\in\mathbb{N}$ let
$\FC{\alpha}^c\eqdef\bigcup_{p\in\FGH{\lt\alpha}}\!\!\CC{DTime}\left(F^c_\alpha(p(n))\right)$
Then for all $c$, $2\leq\beta<\alpha$ and limit $\lambda$,
$\begin{aligned}\FC{\beta}^c&\subsetneq\FC{\beta}^{c+1}\\
\FGH{\beta}^\ast&=\bigcup_{c}\FC{\beta}^c\subsetneq\FC{\alpha}\\
\FGH{<\lambda}^\ast&=\bigcup_{\beta<\lambda}\FC{\beta}\subsetneq\FC{\lambda}
\end{aligned}$
As a corollary, there are no $\FGH{\alpha}$-complete nor $\FGH{<\alpha}$-complete problems. In particular, no $\CC{Elementary}$ nor $\CC{Primitive-Recursive}$ complete problems.
A Catalog of Problems
... in wordle form for $\CC{Ack}=\FC{\omega}$:
Concluding Remarks
numerous high-complexity problems
need for complexity classes:
completeness statementsreductions from a catalog of problems
$\FC{\alpha}$: problems with termination relying crucially on the well-foundedness of $\omega^\alpha$
more in