TD5 - Automates et Langages - RICM

Propriétés des langages réguliers

Exercice 1. Opérations sur les langages et les automates.

Soient L = ab(a+b)* et M= (a+b)*ba - deux langages sur {a,b}. Pour commencer construisez les automates qui reconnaissent L et M.

Trouvez les expressions et les automates pour les langages suivants:

• L U M, LM, L*
• ¬L (complément), ¬M
• L^M (intersection).

Construisez l'automate et l'expression régulière pour le langage de tous les mots ne contenant pas aba (exercice 2, TD4, vous vous rappelez ?).

Construisez l'automate pour (a+ab)*b* ^ ((a+b)(a+b))*.

Exercice 2. Testes sur les langages.

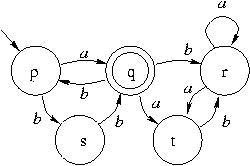
• Est-ce que l'automate dans la figure ci-dessous a le langage non-vide ? A-t-il le langage fini ? Quelle transition faut-il enlever, pour que le langage soit fini?

• Soient L = (00+1)* et M = (001+11)* deux langages. Vérifiez que M est inclus en L.

Exercice 3. Le miroir.

On utilise la notation w^R pour le mot w "renversé". Par exemple, papa^R=apap. Cette opération peut être étendue sur les langages - par exemple ((ab)*)^R=(ba)*

• Trouvez l'expression régulière pour ((ab)*(a+bbba)+a*b*)^R
• Trouvez les automates pour les langages de l'exercice 1 renversés
• Prouvez que si L est régulier, alors L^R est aussi régulier (les langages réguliers sont fermés par rapport au renversement)

Exercice 4. Les homomorphismes

• Construire l'automate pour le langage L=(a+bc)*c*
• l'homomorphisme f est défini comme suit: f(a)=0, f(b)=0, f(c)=1
• • calculer f(abbacb) (il faut le définir d'abord)
  • écrire l'expression pour f(L)
  • construire l'automate pour f(L)
• mêmes questions pour g(a)=0, g(b)=00, g(c)=000
• formuler le théorème de fermeture de langages réguliers par rapport aux homomorphismes

TD1 TD2 TD3 TD4

Retour