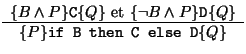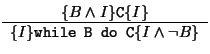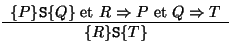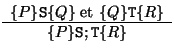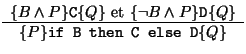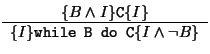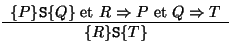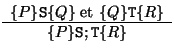Règles

Une autre façon de procéder consiste à ne pas se ramener à la sémantique opérationnelle mais plutôt à définir des règles et de prouver les propriétés des programmes à partir de ces règles.

1. Axiome de l'affectation :
   $\{A[x \leftarrow y]\} \mathtt{x:=y} \{A\}$
2. Règle du IF:
   $\begin{array}{c} \{B \wedge P\} \mathtt{C} \{Q\} \mbox{ et } \{\neg B \wedge P... ...mathtt{D} \{Q\}\\ \hline \{P\} \mbox{\tt if B then C else D} \{Q\} \end{array}$
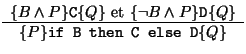
3. Règle du WHILE:
   $\begin{array}{c} \{B \wedge I\} \mathtt{C} \{I\}\\ \hline \{I\} \mbox{\tt while B do C} \{I \wedge \neg B\} \end{array}$
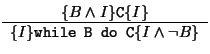
4. Déduction:
   $\begin{array}{c} \{P\} \mathtt{S} \{Q\} \mbox{ et } R \Rightarrow P \mbox{ et } Q \Rightarrow T\\ \hline \{R\} \mathtt{S} \{T\} \end{array}$
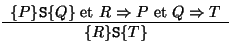
5. Règle de la composition:
   $\begin{array}{c} \{P\} \mathtt{S} \{Q\} \mbox{ et } \{Q\} \mathtt{T} \{ R \}\\ \hline \{P\} \mathtt{S;T} \{R \} \end{array}$

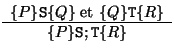
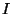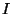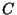Dans la règle du WHILE, $I$ est un invariant: si $I$ est vrai au début de l'itération (et que la condition $C$ est vérifiée, alors 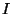$I$ reste vrai après avoir effectué le corps de la boucle.