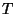m:=a;
n:=b;
while m != n do
if m > n then m := m - n fi
if m < n then n := n - m fi
od
En fait, le texte commenté ci-dessous permet de suivre la preuve. Dans cette présentation, le lecteur a toutes les informations qui lui permettent de reconstituer la preuve.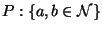
m:=a;
n:=b;
while m != n do
if m > n then m := m - n fi
if m < n then n := n - m fi
od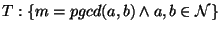
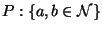
m:=a;
n:=b;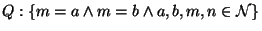
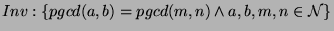
while m != n do
if m > n then m := m - n fi
if m < n then n := n - m fi
od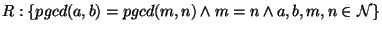
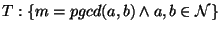
Prouvons d'abord:
(A)
m:=a;
n:=b;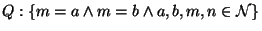
Preuve: Il suffit d'appliquer l'axiome de l'affectation:
Prouvons maintenant:
(I)
if m > n then m := m - n fi
if m < n then n := n - m fi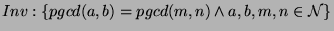
Preuve: On a (axiome de l'affectation):
On en déduit (en utilisant la règle de composition) (W)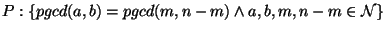
n := n - m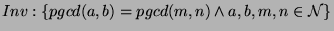
et(théorème)
Et donc (if):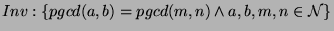
if m < n then n := n - m fi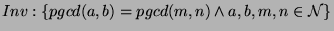
De même on montre que: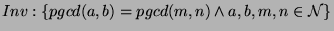
if m > n then m := m - n fi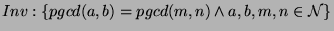
En utilisant la règle du WHILE à (W) on a:
(B)
while m != n do
if m > n then m := m - n fi
if m < n then n := n - m fi
od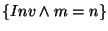
Prouvons enfin:
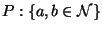
m:=a;
n:=b;
while m != n do
if m > n then m := m - n fi
if m < n then n := n - m fi
od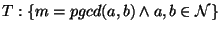
Preuve: Comme
(C)
On déduit que (Règle de déduction appliquée à (B) et (C):(D)
while m != n do
if m > n then m := m - n fi
if m < n then n := n - m fi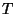
De même de:(E)
On déduit que (Règle de déduction appliquée à (D) et (E):(F)
while m != n do
if m > n then m := m - n fi
if m < n then n := n - m fi
od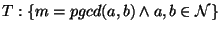
Enfin, par la règle de composition appliquée à (E) et (A):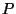
m:=a;
n:=b;
while m != n do
if m > n then m := m - n fi
if m < n then n := n - m fi
od