I am interested in almost any interesting problem!
My specialty is graph theory, in particular graph coloring.
Recently the focus of my research is the development of the theory of homomorphism for signed graphs. This notion would allow us to extend or strengthen results of homomorphism nature for minor closed families, such as the four-colour theorem.
If we take a planar graph and replace each edge with a dense bipartite graph, then the result is still four colorable, but the 4-CT cannot be applied directly. The notion of signed graphs will provide tools to introduce theorems or conjectures in this direction.
An example of questions I look at is given below. For more details on this project please go to: HOSIGRA
For which graphs H the H-coloring problem restricted on planar graphs in polynomial time?
For example, the four-color theorem implies that K4 is such an example:
Given a planar graph check if it has a loop; if it does, then say NO, otherwise YES.
On the other hand, we do not expect such an algorithm for K3 as 3-coloring of planar graphs in NP-complete.
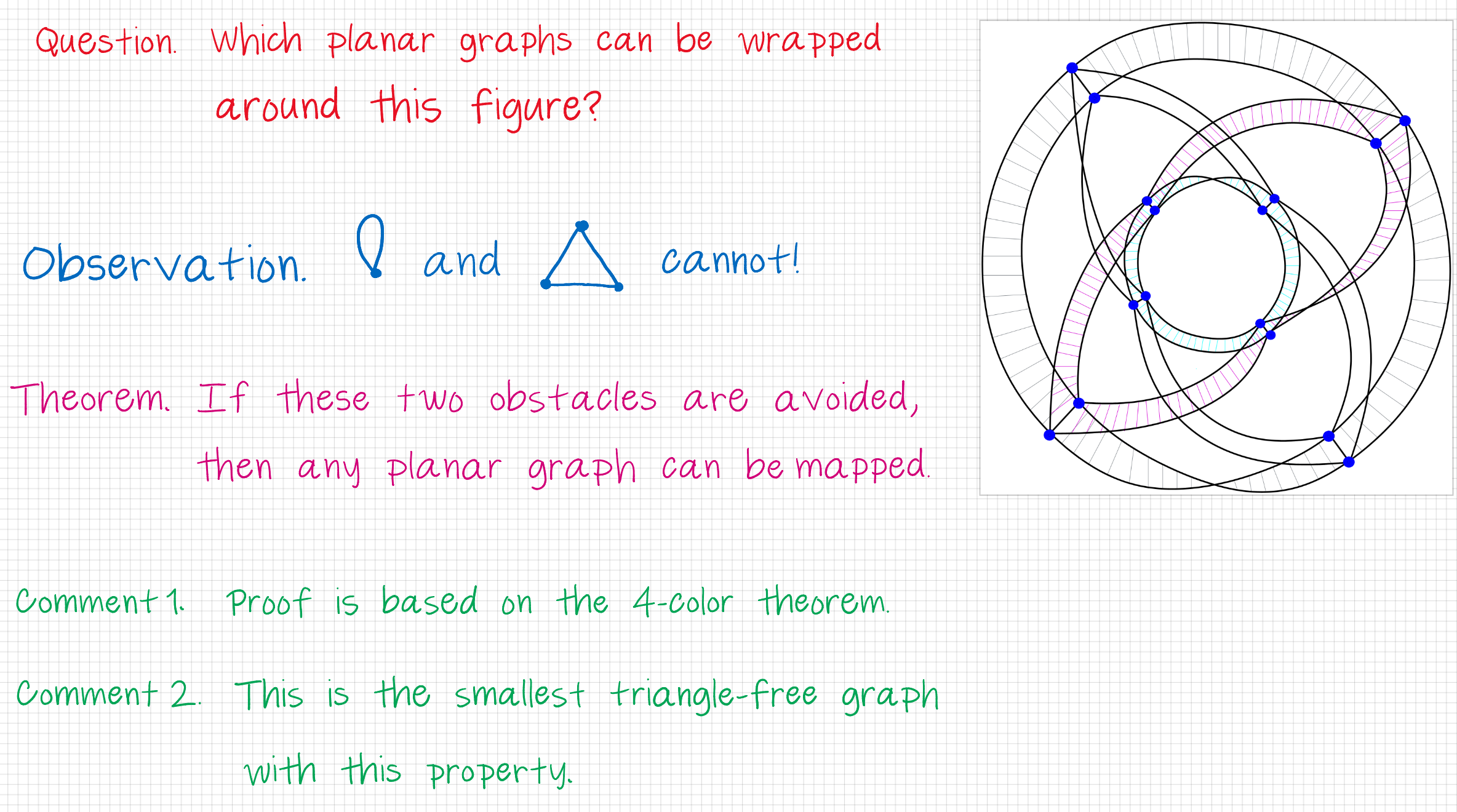
Among the triangle-free graphs H, the smallest one for which we have a polynomial time algorithm is the Clebsch graph (better explained in the image below). The Signed Projective Cube of dimension k is expected to be the smallest signed graph with such a polynomial time algorithm and having no negative cycle of length smaller than k.
This particular case of projective cubes is strongly related to some deep conjectures, in particular to the problem of edge-chromatic number of planar multigraphs and to the characterization of binary clutters on both of which P. Seymour has conjectures which largely generalize the four-color theorem.